|
○ 8163419くん、045くん、その後、レポートが出てきませんが、単位はいらないのですか??
041くん、044くん、レポート受け取りました。
○ 8/5(水)は、急遽、出張が入ってしまい、不在になります。次は、8/10(月)に来ます。呼び出しの応答がよくありません。友人が入っていたら、連絡してあげてください。
○ 採点が終了しました。以下の学生さんはレポートと口頭試問次第です。メールなどで連絡の上、8号館528室に面接に来てください。(下3桁)(連絡が取れましたら、リストから削除します)
019(非常に厳しい)、027(かなり厳しい)
問2が不十分な答案です、点数は足りていますが、このままでは単位は出ません。レポートを持って手渡して下さい。その場でチェック・試問します。
039
○ 8163386 君は放棄ですか?
○ 良く見受けられる間違いとして、振り子で、速度 v を dθ/dt と置いているケースです。これですと、左辺は [m/s] なのに、右辺は [1/s] と次元が合わないので、等号では結べません。弧の長さ、x = lθ ですので、v = l dθ/dt としなければいけません。
○ もう一つは、問2でエネルギー積分をしてもらいました。その際に、両辺を同一範囲で定積分するわけですが、どういう訳か、更に、積分定数 C を付けているケースを良く見受けます。不定積分で積分定数が出てくる理由は、「どこから、何処まで」積分するのか範囲を指定していないので、その(種々の異なる初期条件に対応した)自由度を積分定数として残す必要があるからです。定積分の場合には、両辺で同一の変数範囲(問2では、θ1 からθ2 まで)で積分するので両辺を結ぶ「等号:=」が成り立ちます(即ち、特定の初期条件を代入したことに相当)。この等号を満たすためには、余分な自由度は必要ありませんので、注意して下さい。(積分定数 C が定積分の下限に相当する)(7/26)
エネルギー積分のところで、速度の方が不定積分で、θの積分だけ定積分になっているケースも見受けられます。片辺を定積分にしたら、それに等号で結べるもう一方の辺には任意定数でなく、定積分の積分範囲に対応した定数のみしか許されません。定積分にする時には、両辺揃って定積分にする必要があります。
 |
○ 未だ、採点は始まっていません。とりあえず、2番のc)を解説します。
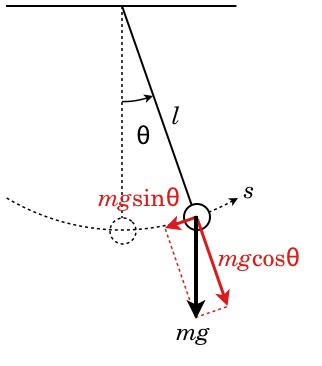
右図のように(力はベクトルの長さを表します)、振り子の運動は、半径 l の円弧上に束縛されているので、その弧上に曲線座標 s を取ると、実質的に1次元的な運動になります。それに垂直な軸方向の運動は、常に糸の張力と釣り合っていて、半径 l は一定に保たれます。質点の速度は s 方向成分のみで、 v = ds/dt。運動方程式は、
m d2s/dt2 = - mgsinθ
これを、θ1 (v1(θ1)) から θ2 (v2(θ2)) まで、両辺に v = ds/dt を掛けてエネルギー積分する:
mv d2s/dt2 = mv dv/dt = - mgsinθ ds/dt
ここで、右辺を積分するために、s = lθ、ds = l dθ の変数変換をすると、
∫ mvdv = - mgl∫ sinθ dθ
mv22/2 - mv12/2 = mgl (cosθ2 - cosθ1)
ここで、右辺に (1-1)(勿論、ゼロです)を加えて位置エネルギーの形に変えると、
mv22/2 + mgl (1-cosθ2) = mv12/2 + mgl (1-cosθ1) = const.
の、エネルギー保存則が得られます。2番の d), e) は、単振動のプリントにあるとおりです。
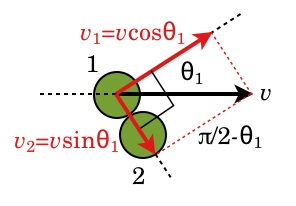 |
○ 次は、3番の b) です。講義では、衝突後のそれぞれの球の速度は考えませんでした。しかし、弾性散乱であれば、右の図のように幾何学的に決まります。質量が等しい2つの円盤の衝突後に、互いになす角が π/2 であることは講義でも見てきたし、プリントにも議論されています。右図のように、速度 v で運動してきた円盤を1とすると、衝突後の散乱角は θ1 と書けます。この図から、v1 と v2 の v 方向成分の和が v になり、元々、運動量を持っていなかったそれに垂直な成分がゼロになることは、容易に確かめられます。
実際に、問題を解く時には、運動量保存則の v 方向成分の保存則と、それに垂直な方向の保存則を連立させて解くことになります。各自で確認をしてください。v 方向を x, それに垂直な方向を y とすると、
vx = v = v1 cosθ1 + v2 sinθ1
vy = 0 = v1 sinθ1 - v2 cosθ1
これらを連立させて、v1 或いは v2 を消去すれば求まります。
○ 強制振動のプリントをアップしました。講義の内容に沿った版です。
○ 次回は、13日(月)(演習を講義に振り替え)と14日(火)の2日連続です。
○ 前回のレポート、台風の遠心力と、地球の自転による台風に働くコリオリ力の比較ですが、どうも、半径300 kmで風速40 m/s では、ほぼ同じ大きさになるようです。数倍から1桁位遠心力が大きいと思っていました。台風の内側に入っていくと、半径が小さくなり、風速も増すので、だんだん遠心力が勝ってきますが、この半径ですと、遠心力と同程度でした。多分、ωを求める時に2πを忘れたのでしょう。
コリオリ力の例:台風のプリントも修正。
○ 回転の運動方程式のプリントを一部修正しました。
○ 本日(6/30)のレポートは、台風の中心から半径 300 km で風速 40 m/s の時に、その円運動による遠心力と、地球の自転によるコリオリ力を計算し、それらの比から、遠心力が勝ることを確認せよ、です。
○ コリオリ力の例のプリントの修正版で、P-P0=2ΔP0/(1-(r/r0)) としています。係数の2は新たに加えたのですが、その意味は、r=r0 が台風の目の半径と考えた時に、その位置で気圧が P-P0=ΔP0 となる様に定義するため、分母の2を打ち消す事です。
○ コリオリ力の例のプリントをまた修正しました。特徴的半径 r0 以下になると遠心力が勝ってきて、風速が減少してきます。これが台風の目が出来る理由のようです。
これは、ブラックホールが出来るのと同じ理由です。光でさえ光速以上で動けないので、遠心力が増えなくなり、引き込まれていきます。
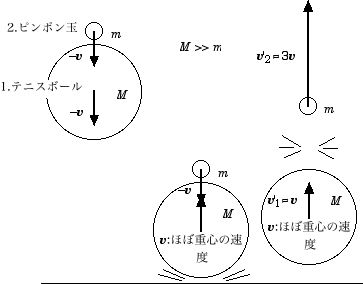
○ 本日(6/23)の宿題は、親子ボールの解析です。右図のように、質量が大きいテニスボールと、軽いピンポン球を重ねて弾ませた時、テニスボールの弾み方はあまり変化しないが、ピンポン球はテニスボールの上に載ったまま床で弾むと、通常の高さよりも10倍近く高く弾む。この実験結果を、全て弾性衝突だと仮定して、エネルギー保存則と運動量保存則を解くことにより、解析せよ。
この時、考察するのは右の図の中央の状態で、テニスボールだけが床で跳ね返って、ピンポン球と正面衝突した瞬間を解析する。この瞬間の保存則を考えるので、位置エネルギーの変化は無視して良い。
○ 平均点は73点でした。
例年、「お!前期は頑張ってるなあ!」と感じた学生さんの内の何名かは、期末試験で墜落しています。油断大敵ですので、よろしく。
○ 未だ、途中ですが、これまでに何回か質問に来てくれた学生さんが良い点を取ってくれました。感激です!そう、あなたも、質問を活用しましょう。
○ やっと採点を開始しました。問2の「tL」には「L」を含まなければいけない、と言う点は勘違いでした。当然ながら、「h」だけ落ちる時間にも等しくなければいけませんので、両方の表現が可能で、「L」或いは「h」を含まなければいけない、が正しい説明でした。
○ 来週の6/9は中間テストです。内容は、先週下に書いたとおりです。なので、宿題はありません。(6/2)
今日の講義で、単振動の発見的解法の最初の初期条件の特解の速度に負号が抜けいていました。
x(t) = x0 cos ωt, v(t) = -x0ω0 sin ωt.
また、複素平面上のベクトルに、虚数 i を掛けると π だけ回転することは、
i = eiπ
を用いて、
i eiωt= eiπ×eiωt = ei(ωt+π)
となることは直感的で分かりやすいです。
○ 摩擦がある場合の飛距離の見積を「空気抵抗:投げ上げ」の p.3-p.4 にアップしました。色々と符号の間違いがありました。それから、対数のマクローリン展開は、今日、沢山質問した最前列の君(ご免、未だ名前覚えてない)が正しいことを確認しました。
○ 6月9日(火)に小テストを予定しています。これまでに、講義で扱った問題、レポートで考えてもらった問題などを理解していれば出来る内容です。運動法則、投げ上げ問題、まさつ、単振動(次週やります)等、座標を書き、外力が何かを考えて運動方程式を立て、その微分方程式を変数分離や特性方程式などを用いて解く、ことが目標です。
○ 6月2日提出のレポートです。
1)断面積 S が1m2 の板に、風速 30 m/s の風が垂直に当たっている。この時に、板が受ける力を以下の仮定の下で計算しなさい:空気の、単位時間あたりの板に垂直な運動量成分(ΔP/Δt = (ΔM×v)/Δt )が、板に当たった時に、板から受ける力により全て失われるとしよう。ここで、空気の密度 ρ は 1.3 Kg/m3、ΔM = ρSv である。
なお、単位の明記を忘れずに。また、力 [N] を重力加速度 g で除して得られる [Kg重] で表現すると、どの程度の力が働くのか感覚的に理解しやすくなる。
2)余裕があれば、慣性抵抗が働く時の雨滴の終速度を計算する。条件は、前回と同じ。ただし、この時の面積は雨滴の断面積を取る(球の表面積ではない)。
○ 5月26日(火)提出のレポートです。前回のレポートを採点していますが、1)と被っているようです。前回のレポートで既に1)の解答をした場合には再度提出の必要はありません。その旨、書いてもらい、2)だけ解いてください。
1)速度に比例する粘性抵抗、-cv、が働く時の自由落下の運動方程式を解きなさい。
dv/dt = -g - cv/m = -(c/m)(v+ mg/c)
が運動方程式。V = v+ mg/c と変数を変換すれば dV/dt = dv/dt なので、変数分離法により容易に解が求まる。時刻 t の時の、速度 v、位置 r を求めよ。
2)粘性抵抗、Ff = - cv、c = 6πaη、がある時に、半径 a が 1 mm の雨滴の落下速度を考える。簡単のために、終端速度を計算する。即ち、上式の dv/dt = 0 を考えると、正味の力はゼロなので、等速度 vf = - mg/c で落下し、重力と摩擦力が等しくなった状態に相当する。
ここで、η = 1.8×10-5 (Pa•s)、g = 10 (m/s2)、水の密度 ρ = 103 (Kg/m3) を用いよ。
余裕のある人は、運動方程式から、1,000 (m) 上空から落下してきた雨滴の、地表における速度を出してみてください。
○ まず最初に、レポート点を付けていますので、遅れても、レポートは提出する方が良いです。よろしく。
○ 前回の宿題のところで、緯度を36度にしました。これは、遠心力には効きますが、万有引力は地球の中心との距離が効きますので、万有引力には cosθは不要です(私が下に書いた式には cosθを入れ忘れていました)。なお、
F万有 = mg
なので、質量に50 Kg を代入した場合は、約500 N になるはずです。確認してみてください。下に与えた1桁の精度の数値を代入すると、重力加速度が 11 m/s2 程度になるので、これを使うと、約550 N です。なお、
F遠心/F万有 ≈ 2×10-3
となりますので、g = 9.8 m/s2 の精度でしたら、遠心力は無視できることになります。
さて、来週(5/19)提出の宿題は、
1) 空気摩擦が無い時には、45度の角度で投げあげると、最も遠くまでボールを飛ばせることが分かりました。何故なら、ボールの高さがゼロになるときの水平距離が
x = (v02/g)2sinθcosθ (1)
になるからです(質点の運動 のプリント参照)。
さて、それでは、空気摩擦がある時には、この角度をどの様に変化させる、或いは変化させないのが良いでしょうか。各自の考えをレポートにまとめてください。速度に比例する摩擦がある場合の運動方程式、
dv/dt = mg - Cv
を使っても構いません。ここで、C > 0、g は、重力加速度ベクトルとします。なお、摩擦力ですので、右辺の - Cv は常に負でなければならない点に注意してください。
2) ボールを100 mまで投げたいとする。投げあげ角を45度にしたときには、初速を幾らにすればよいか?式 (1) を使って求めなさい。
次に、角度を、自分の生まれ月×10 度の場合には、初速は幾らになるか?ただし、自分の生まれ月 > 8月、即ち、9月以降の時には、自分の生まれ月×10-80 度とします。
○ 板書の最後の部分で、d2r/dt2 = F は、= F/m の m の書き忘れでした。訂正をお願いします。
○ 5/12(火) 提出のレポートは、北緯36度 の地表において、球として近似した地球による万有引力の大きさと、地球の自転による遠心力の大きさの比(F遠心/F万有) を計算することです。
これにより、近似的に万有引力のみを考慮すれば、地表における物体の運動は、ニュートンの第二法則の、慣性系の運動方程式で書けることになります。
重力と遠心力は、下の式を用いて計算して下さい。
F万有 = GM地m物体/R地2
F遠心 = m物体R地•cosθ•ω地2
ここで、G = 7×10-11 [N•m2/kg2]、M地 = 6×1024 [kg]、R地 = 6×106 [m] としても良い。
○ 4/28提出のレポート課題は、ベクトル三重積の展開の導出です。ベクトルの成分で表示して導いてください。
A × (B × C) = (C•A) B - (A•B) C
○ 講義はプリントを主体に進める予定です。参考書としては、
- 物理学:原 康夫著:学術図書出版社(物理全般、易)
- 力学:戸田盛和著:岩波書店(力学、中)
- ファイマン物理学 I:ファイマン・レイトン・サンズ 共著:岩波書店(力学他、面白いけど難)
- 解析概説:高木貞治:岩波書店(物理で使う数学の友。学生の時に神田の本屋で客に勧められて購入)
等がお勧めです。教科書代わりには、1か2が良いでしょう。
|