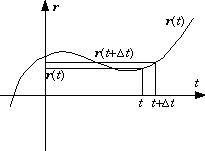
平均の速さ $v$ は、$\Delta t$ の間に進んだ距離を $\Delta t$ で割ることにより得られる;$\large{v=\frac{\Delta x}{\Delta t}}$.しかし、もっと一般的に、位置座標 $\boldsymbol r(t)$ は時間 $t$ の関数として連続的に変化するので、ある時刻 $t$ における速度 $\boldsymbol v(t)$ や加速度 $\boldsymbol a(t)$ を考えるためには、時刻 $t$ の微係数として速度・加速度を定義する必要がある.
速度:$$\large{\boldsymbol v(t)=\lim_{\Delta t \to 0}\frac{\boldsymbol r(t+\Delta t)-\boldsymbol r(t)}{\Delta t}=\frac{d\boldsymbol r(t)}{\Delta t}=\left(\frac{dx}{dt},\ \frac{dy}{dt},\ \frac{dz}{dt}\right)}$$ |
加速度:$$\large{\boldsymbol a(t)=\frac{dv}{dt}=\frac{d^2\boldsymbol r}{dt^2}=\left(\frac{d^2x}{dt^2},\ \frac{d^2y}{dt^2},\ \frac{d^2z}{dt^2}\right)}$$ |
 |
円運動の例:2次元極座標表示
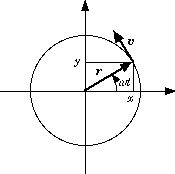 |
半径 $r$ の円周上を等速で運動する場合:位置ベクトルの長さ $r$ 及び角速度 $\omega$ は時間的に変化しないため、
$$\large{\boldsymbol r(t)=(x,\ y)=(r\cos \omega t,\ r\sin \omega t)=r(\cos \omega t,\ \sin \omega t),}$$ $$\large{\boldsymbol v(t)=\frac{d\boldsymbol r}{dt}=r\omega(-\sin \omega t,\ \cos \omega t),}$$ $$\large{\boldsymbol a(t)=\frac{d\boldsymbol v}{dt}=-\omega^2r(\cos \omega t,\ \sin \omega t)=-\omega^2\boldsymbol r \quad (=\boldsymbol\omega\times\boldsymbol v=\boldsymbol\omega\times(\boldsymbol\omega\times\boldsymbol r)}\text{: 中心を向いた「向心加速度」})$$これより、加速度ベクトルは位置ベクトルと平行で逆向きだと分かる.角速度ベクトル ωは軸性ベクトルで、大きさは ω、方向は回転軸に平行で右ネジの進む方向に取る.
速度ベクトルと、位置ベクトル、或は加速度ベクトルとの内積
$$\large{\boldsymbol v(t)\bullet\boldsymbol r(t)=r^2\omega(-\sin\omega t,\ \cos\omega t)(\cos\omega t,\ \sin\omega t)=r^2\omega(-\sin\omega t\cos\omega t+\cos\omega t\sin\omega t)=0,}$$ $$\large{\boldsymbol v(t)\bullet\boldsymbol a(t)=-r^2\omega^3(-\sin\omega t,\ \cos\omega t)(\cos\omega t,\ \sin\omega t)=-r^2\omega^3(-\sin\omega t\cos\omega t+\cos\omega t\sin\omega t)=0,}$$がゼロになることから、どちらのベクトルとも互いに直交していることが確認できる.