HOME |
ベクトル |
大きさと方向を持つ量(少なくとも2つ以上の成分を持つ量)をベクトル量と呼び、大きさのみを持つスカラー量と対比して用いられる.
 |
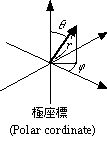 |
表記例(位置座標)
直交座標:(x, y, z)、 極座標:(r, θ, φ)、 記号:V , 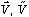
ベクトルの基準点は任意の位置に置いて良い.
極性ベクトルと軸性ベクトル
本来方向を持つ量を表すベクトルを極性ベクトルと呼ぶ
例)変位ベクトル、速度ベクトル、力ベクトル
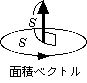 |
本来方向はないが、適当な約束でその方向を定めたベクトルを軸性ベクトルと呼ぶ
例)面積ベクトル、角速度ベクトル
2つのベクトルを a=axi+ayj+azk、b=bxi+byj+bzk とする.
和、差
a±b = (ax±bx)i+(ay±by)j+(az±bz)k
内積(スカラー積、積はベクトルではない)
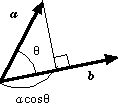 |
a•b=ab cosθ,
i, j, k を直交座標の3つの単位ベクトルとすると、これらは互いに直交するので、
i•i=j•j=k•k=1, i•j=j•k=k•i=0
となる.従って、
a•b=(axi+ayj+azk)(bxi+byj+bzk)=axbx+ayby+azbz
が得られる.
ベクトルの長さ:a=(a•a)½=(ax2+ay2+az2)½
外積(ベクトル積、積はベクトル)
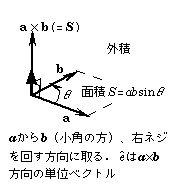 |
|a×b|=ab sinθ, 方向は右図の通り.
従って、平行なベクトルの外積はゼロになる.
i×i=j×j=k×k=0,
i×j=-j×i=k, j×k=-k×j=i, k×i=-i×k=j
が成り立つ.従って、
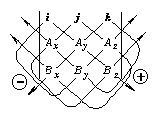
a×b=(axi+ayj+azk)×(bxi+byj+bzk)
=(aybz-azby)i+(azbx-axbz)j+(axby-aybx)k
が得られる.
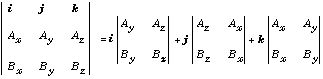 |
 |
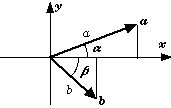 |
外積を用いて三角関数の加法定理を求める.
a=a(i cosα + j sinα)、b=b(i cosβ - j sinβ)とすると、
b×a=b(i cosβ - j sinβ) × a(i cosα + j sinα)
=ab(i×i cosβcosα +i×j cosβ sinα - j×i sinβcosα - j×j sinβsinα)
=ab(sinαcosβ + cosαsinβ)k
外積の定義から、b×a=kabsin(α+ β) なので、
sin(α+ β) = sinαcosβ + cosαsinβ
が得られる.
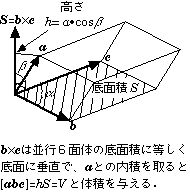 |
a•(b×c)= a•S=Sa cosβ=V=(a×b)•c=[abc],
ここで、a cosβ はベクトル abc で作る平行6面体の bc で張る底面から測った高さ h に等しい.[abc] は、グラスマンの記号と呼ばれ、abc を cab、bca と順番に入れ替えても結果は変わらない事を意味する.しかし、交換するとマイナスがつく.その大きさは、左の図に示すように、3つのベクトルで張る並行6面体の体積を与える.
a×(b×c)=[a[bc]]=b(a•c)-c(a•b)
(a×b)×c=–c×(a×b)= –a(c•b)+b(c•a)
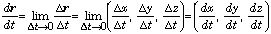
ベクトルの微分の成分は、成分の微分.円運動の場合は、半径の長さr は一定なのでその2乗(内積、r•r=C)も一定.それを時間で微分すると、
d(r •r)/dt = dC/dt = 0, ∴ (dr/dt)•r + r•(dr/dt) = 2r•(dr/dt) = 2r•v = 0, ∴ r ⊥ v
が得られ、半径ベクトルと速度ベクトルは常に直交していることが分かる.等速円運動の場合は速さv も一定なので、全く同様にv•a=0が得られ、速度と加速度が直交していることが示される.
1)スカラー変数による積分:
例:移動量(ベクトル量)
∫ vdt=(∫ vxdt, ∫ vydt, ∫ vzdt)
2)内積の積分(接線線積分)
例:仕事量(スカラー量.)
点AからBまでの接線線積分
∫ ABF•dr=∫ ABFxdx + ∫ ABFydy + ∫ ABFzdz
3)面 積分(スカラー量)
面Sの上の面積分
∫SA•dS=∫SA•ndS
S は面積ベクトル、n は面の法線(面積)単位ベクトル.
 |
4)体 積分(スカラー量)
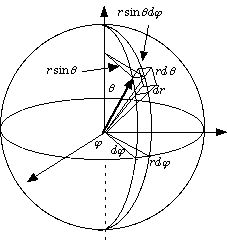
∫φdr=∫φdV=∫∫∫φdxdydz=∫∫∫φr2sinθdrdφdθ
体積要素(右図参照):dV=dxdydz=r2sinθdrdφdθ
*ガウスの発散定理:∫VdivAdv=∫SA•dS(体積分 => 面積分)
*ストークスの定理:∫SrotA•dS=∫CA•ds (面積分 => 線積分)
問
1)スカラー三重積とベクトル三重積の成分を書き下し、ベクトル三重積の(A)式を確認せよ.
2)cos(α + β) = cosαcosβ–sinαsinβをベクトルを使って証明せよ.
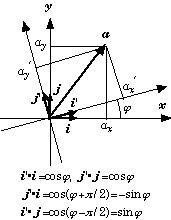 |
a=axi+ayj=ax'i'+ay'j' に i, j のスカラー積をとると
ax=ax'i'•i+ay'j'•i=ax'cosφ - ay'sinφ
ay=ax'i'•j+ay'j'•j=ax'sinφ + ay'cosφ
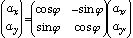
∇ = i ∂/∂x + j ∂/∂y + k ∂/∂z
gradφ = &nablaφ = i ∂φ/∂x + j ∂φ/∂y + k ∂φ/∂z = (∇xφ, ∇yφ, ∇zφ)
 |
例)保存力
U を重力や電場などのスカラーポテンシャルエネルギーとすると、働く力Fは
F= -∇U(r)=(-∂U/∂x, -∂U/∂y, -∂U/∂z)=(Fx, Fy, Fz)
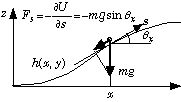
で与えられる.例)z=h(x, y) 、U=mgz とすると、 F= -∇U(x, y)= -mg(i ∂h/∂x + j ∂h/∂y + k ∂h/∂z)= -mg(i ∂h/∂x + j ∂h/∂y)= -mg(i tanθx + j tanθy) 任意の方向 s(単位ベクトル)の力の成分は力との内積を取って、 Fs= -s•F= -mg(s•i tanθx+s•j tanθy)
で得られる.右図の様にx-z 面内で s がh(x, y) の接線になっている場合は s•i=cosθx 、s•j=0 なので(一般的には方向余弦になる)、Fs= -mg sinθx が得られる.これは、直接求めたFs= -(∂U/∂s)= -mg sinθx に等しい.
☆ベクトルの方向微係数・発散 (Divergence)
divA = ∇•A = ∂Ax/∂x + ∂Ay/∂y + ∂Az/∂z
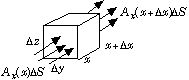
発散の意味は、微少体積(Δx, Δy, Δz)から出てくる(電荷から出る電気力線の様な)湧き出しを表す.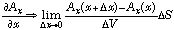 と書くと、Ax(x+Δx)ΔS がx+Δx の位置の微少面積ΔS=ΔyΔz から出ていく量で、x の位置の微少面積ΔS から入るAx(x)ΔS を引き、体積ΔV で割っているので、ゼロにならない分が単位体積から湧き出す量になる.他の成分も同様に理解できる.
と書くと、Ax(x+Δx)ΔS がx+Δx の位置の微少面積ΔS=ΔyΔz から出ていく量で、x の位置の微少面積ΔS から入るAx(x)ΔS を引き、体積ΔV で割っているので、ゼロにならない分が単位体積から湧き出す量になる.他の成分も同様に理解できる.
gradient の発散
div∇φ = ∇•∇φ = ∇2φ = Δφ = ∂2φ/∂x2 + ∂2&phi/∂y2 + ∂2φ/∂z2
ナブラの発散 ∇2=Δ は、ラプラス演算子、ラプラッシアンと呼ばれる.
(参考)ラプラス方程式:∇2φ=Δφ=0、ポアッソン方程式:∇2φ=ρ(ρは電荷密度)
ナブラとベクトルの外積
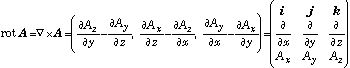
また、A=rotB の時、B を A のベクトルポテンシャルと呼ぶ.(スカラーポテンシャルと比較)