質点の運動
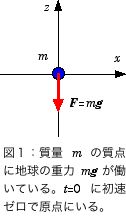 |
地上に於ける質点 m の運動を考えよう。t=0 に初速ゼロで図1の原点にいる。まずニュートンの第2法則を使って運動方程式をたてる必要がある。運動方程式を解く最初の例なので、なるべく丁寧に式を追っていくことにする。
| dP/dt = F | (1) |
ここで、P=mv は運動量。最初に速度を考えよう。そうすると、第2法則の中で、与えられているパラメーターは外力 $\boldsymbol F$ であり、地球の重力を代入する。この時に大事な点は、どの様な座標系でこの運動を取り扱うのか、と言うことを明確に定義しておくことである。ここでは、図1のように、鉛直上方を y 軸にとる。力 F をベクトルのまま第2法則に代入すれば、重力加速度ベクトルを g=(0, 0, –g) として、
| dP/dt = mg |
或いは、
| dv/dt = g | (2) |
が求める運動方程式になる。次に具体的に速度 v=(vx, vy, vz)、位置座標 r=(x, y, z) についてこの微分方程式を解く。そのためには更に具体的に、運動方程式を x-、y-、z-成分に分けて表しておくのが便利である。すなわち、
| dvx/dt = 0 | |
| dvy/dt = 0 | (3) |
| dvz/dt = –g |
を連立させて解く。と言っても、この問題は実質的に1次元運動であり、他の2つの方向の初速度=ゼロを考慮すれば、z-成分のみを解けばよい。(3) の両辺を時間 t で不定積分して、一般解(積分定数を含み、どんな初期条件の場合の解も含む広い解)が
|
vx= Cx | |
| vy= Cy | (4) |
| vz= ∫ dvz= –g ∫ dt = –gt + Cz (Ci:積分定数. i = x, y, z) |
と得られる。x, y 成分は重力の成分がゼロなので、積分定数のみ。
位置座標 r は、(4) 式を時間についてもう一度不定積分して、一般解が
| x = ∫ vxdt= Cxt + C'x | |
| y = ∫ vydt = Cyt + C'y | (5) |
| z = ∫ vzdt= –g ∫ t dt =–gt2/ 2 + Czt + C'z (C'i:積分定数) |
と求まる。初速度 v(t=0) = v0 = 0 から、Cx = Cy = Cz = 0 なので、速度の特(別)解が、
| vx = vy = 0, | |
| vz = –gt |
と求まり、位置座標は
| x = C'x | |
| y = C'y | (6) |
| z = –gt2/ 2+ C'z |
で、t=0 で r=0 の初期条件を代入して、C'x = C'y = C'z =0 から位置座標の特解が
| x = 0 | |
| y= 0 | (7) |
| z = –gt2/2 |
投げ上げの例
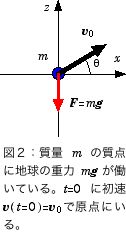 |
次に図2の、水平面に対して角度 θ で投げ上げる例を考えよう。前の例と違う点は、初速度がゼロでない点のみである。従って、初期条件を代入して特解を求める前の一般解、(4), (5) が、そのままこの例でも使える:
| vx= Cx | |
| vy= Cy | (4) |
| vz= ∫ dvz=–g ∫ dt =–gt + Cz (Ci:積分定数. i = x, y, z) |
及び、
| x = Cxt + C'x | |
| y = Cyt + C'y | (5) |
| z =–gt2/ 2 + Czt + C'z (C'i:積分定数)。 |
そこで、順番に初期条件を代入して図2の場合の特解を求めよう。 t=0 で v(t=0) = v0 = (v0 cosθ, 0, v0 sinθ) なので、速度の特解は、
| vx= v0 cosθ | |
| vy= 0 | (8) |
| vz=–gt + v0 sinθ |
となる。同様に、位置座標は t=0 で r=0 なので、C'x = C'y = C'z =0 から
| x = v0t cosθ + C'x = v0t cosθ | |
| y = C'y = 0 | (9) |
| z =–gt2/ 2 + v0t sinθ + C'z =–gt2/ 2 + v0t sinθ |
と決まる。
x と y の関係
次に、ある時刻 t の時の x と z の関係を、時刻 t を消去して調べよう。(9)-1 から
| t = x /v0cosθ |
なので、
| z = –gx2 /2v02cos2θ + x•tanθ | (10) |
の x の2次関数の関係、放物線運動が得られる。
この式から、空気抵抗がない時に、θ を何度にすると最も遠方まで飛ぶかを確かめることが出来る。地面に落下したときに z = 0 なので、x について整理すると、
|
x = 2v02•cosθsinθ /g = (v02/g ) sin2θ |
なので、sin2θ が最大になる θ = π/4 の時に最も遠方の v02/g まで飛ぶ。面白いことに、この距離は、真上に初速 v0 で投げ上げたときの高さ v02/2g の、丁度2倍になっている。
問 良く知られているように、最も遠くまで投げるには、45度の角度で投げるのが良い。さて、実際には、空気抵抗がある。この場合は、最長飛距離を出すには、角度を増せばよいか?それとも小さくすべきだろうか?
# 07.5.1