
HOME |
地表での質点の運動 |
戻る
このページは"Mathjax"を用いて表示しています。不都合がある場合はこちらをどうぞ。
これから質点の運動を考えるわけであるが、我々が住む地球表面上は、ニュートンの運動法則が前提としている「慣性系」ではない。自転、公転などの回転運動をしているので、「速度、加速度」で見たように常に中心に向かう万有引力に起因する向心(中心に向かう)加速度が働いている。それでは、ニュートンの運動方程式は、地表では役に立たないのだろうか。ここでは、そうではなく、加速度が働いているために生ずる「見かけの力」(慣性力)を導入すれば、慣性系と同じ式が使えることを見ておこう。
図に示した2つの座標系、$xyz$-系(静止している「慣性系」)と $x'y'z'$-系(加速度運動も含む運動をする系)が時刻 $t=0$ に重なっていたとする。$x'y'z'$-系が速度ベクトル $\boldsymbol V'(t)$ で運動しているとき、時刻 $t$ における点 P の $x'y'z'$-系で見た位置ベクトル $\boldsymbol r'(t)$ は、$xyz$-系の位置ベクトル $\boldsymbol r(t)$ を用いて次のように書ける(ガリレイ変換)。
$$\large{ \boldsymbol r'(t)=\boldsymbol r(t)-\int^t \boldsymbol V'(t')\,dt'=\boldsymbol r(t)-\boldsymbol R'(t).\qquad (1) }$$ |
ここで、$x'y'z'$-系の速度 $\boldsymbol V'(t)$ は時々刻々、変化するので、原点の位置ベクトル $\boldsymbol R'(t)$ を得るために速度を時間で積分している。運動している座標系 $x'y'z'$-系から見たP点の速度は、(1)式を時間で微分して、
$$\large{ \boldsymbol v'(t)=\frac{d\boldsymbol r'}{dt}=\frac{d\boldsymbol r}{dt}-\frac{d\boldsymbol R'}{dt}=\frac{d\boldsymbol r}{dt}-\boldsymbol V'(t), \qquad (2) }$$となる。もう一度、時間で微分すると、$x'y'z'$-系上で観測した点 P の加速度
$$\large{ \boldsymbol a'(t)=\frac{d^2\boldsymbol r'}{dt^2}=\frac{d^2\boldsymbol r}{dt^2}-\frac{d\boldsymbol V'}{dt},\qquad (3{\rm a}) }$$が求まる。ここで、$\large{\frac{d\boldsymbol V'}{dt}}$ は、太陽の周囲の公転運動などに対応する地球の速度ベクトル $\large{\boldsymbol V'}$ の時間変化率(加速度)を表す。仮に、この変化率がゼロであれば、時間的に速度ベクトルの長さも方向も変化しない事に対応するので、等速直線運動になる。そのような系は、加速も減速も方向の変化もしない座標系として「慣性系」と呼ばれ、ニュートンの運動法則が成立つ。
一方、地球の様に自転をし、太陽の回りを公転する座標系においては、$\large{\frac{d\boldsymbol V'}{dt}}$ は時間と共に変化する加速度を表している。完全な円軌道の運動であれば、速度ベクトルの方向が時々刻々変化する「加速度運動」になる。(3) 式の第3辺、第一項は、ニュートンの運動方程式が成り立つ慣性運動する $xyz$-系の運動方程式 $\large{\frac{d^2\boldsymbol r}{dr^2}}=\frac{\boldsymbol F}{m}$ から、$\large{\frac{\boldsymbol F}{m}}$ に置き換える事が出来る。また、その第2項の加速度 $\large{\frac{d\boldsymbol V'}{dt}}$ は、慣性系におけるニュートンの運動方程式に倣って「見掛けの力 $\large{\boldsymbol F'}$」を導入して、$\large{-\frac{d\boldsymbol V'}{dr}}=\frac{\boldsymbol F'}{m}$ と置くことが出来る。$\large{\boldsymbol F'=-m\frac{d\boldsymbol V'}{dt}}$ は、$x'y'z'$-系が惑星の公転運動の様な速度ベクトル $\large{\boldsymbol V'}$ の長さや方向が時間と共に変化する 加速度運動をしている時に現れる「慣性力」(例:遠心力)として理解出来る。
この式は運動する系(例:車内や地表面上)で見た点P の運動方程式であるが、見かけ上は慣性系上のニュートンの運動方程式と何ら変わらず、ただ、力として慣性力が加わっている点だけが異なる.半径が $\boldsymbol r'$ で、一定の角速度 $\omega$ の円運動の場合は、速度が $\large{\boldsymbol V'=\boldsymbol\omega\times\boldsymbol r'}$ で与えられるので、加速度、$\large{\frac{d\boldsymbol V'}{dt}=\frac{d(\boldsymbol\omega\times\boldsymbol r')}{dt}=\frac{d\boldsymbol\omega}{dt}\times\boldsymbol r'+\boldsymbol\omega\times\frac{d\boldsymbol r'}{dt}=\boldsymbol\omega\times\boldsymbol v'=\boldsymbol\omega\times(\boldsymbol\omega\times\boldsymbol r')=-\omega^2\boldsymbol r'}$($\large{-\boldsymbol r'}$ 方向(中心方向)を向かう向心力を $\large{m}$ で割った量)と反対向きの「遠心力($\large{\boldsymbol F'=m\omega^2\boldsymbol r'}$、ベクトル $\large{\boldsymbol r'}$ の向き)」が加わっている。結論として、加速度系に相当する地球表面上であっても、(3b) 式のように、実際に働いている力 $\large{\boldsymbol F}$ に加えて、慣性力 $\large{\boldsymbol F'}$ も「力」として働くと考えれば、ニュートンの運動方程式の形はそのまま使えることが分かる。
結局、質点の運動方程式を考えるには、慣性系上か非慣性系(加速度系)かによらず、ニュートンの運動方程式に、遠心力などの慣性力を含めた、質点に働く全ての「実際の力」と「見掛けの力」 $\boldsymbol F_i$ を使い $$\large{ m\frac{d^2\boldsymbol r}{dt^2}=\sum_i\boldsymbol F_i, \qquad (4) }$$
とすれば良いことになる。下に示す例1、2のような場合には、見かけ上大変異なった振舞いをする。地表における質点の運動は、例1とも2とも異なっている。地表の物体は、円運動はしているけれど非常に遅いため、自転による見かけの力(遠心力)$\boldsymbol F'$ は重力より十分に小さい。そこで、通常は遠心力で補正された「重力 $\boldsymbol F$」 を考える。
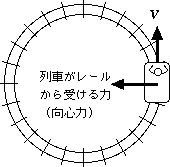 |
(例1)円運動する電車内の質点の運動を考えよう。体験的に良く知っているように、電車がカーブを曲がると、車内の物体はカーブの外側に力を受ける。これは、例2の人工衛星内の物体の運動(仮想的な無重力状態)とは非常に異なっている。その理由は、円運動をするためには、慣性力と大きさが等しく、反対向きの「向心力」が必要な点にある。ところが、向心力は、車輪とレールが擦れることによって生ずるため、電車はレールから向心力を受けて円運動をするのだが、中の物体は慣性の法則が予測する通りに直進するので、電車とは別々の運動をすることになる。即ち、車内に立っている人には床との摩擦により足先のみに向心力が働く。体の重心から大分ずれているため、倒れてしまう。電車と共に運動するためには、直線運動をする重心に向心力を加えるために、吊革で体を支える必要がでる。。
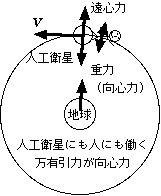 |
(例2)人工衛星内に固定した座標系で成立つ運動方程式も、人工衛星が円運動をする非慣性系なので (3) 式が使える。人間にも人工衛星と全く同様に遠心力 $\boldsymbol F'$ に加えて、遠心力と逆向きで同じ大きさの向心力(地球の引力)$\boldsymbol F=-\boldsymbol F'$ が働いている。結局、(3) 式は $$\large{ m\frac{d^2\boldsymbol r'}{dt^2}=\boldsymbol F+\boldsymbol F'=\boldsymbol F-\boldsymbol F=0, }$$
となり、慣性系において全く重力が働いていないときと全く同じ運動をするように見えることが分る(例:スペースラボ内のボールの運動は、等速直線運動をする)。実際には、人工衛星の重心の位置からはずれると、重力と遠心力のバランスが微妙に崩れるので、微少重力環境と呼ばれる。ところで、スペースシャトルが軌道上を周回している時には、シャトルの向きが地球とシャトルを結ぶ軸に平行になっている。地球による重力と遠心力のバランスから、その理由を考えてみよう。