HOME

ニュートンの運動法則

戻る このページは"Mathjax"を用いて数式を表示しています。不都合がある場合には、こちらをどうぞ。

ガリレオ、ケプラー、ホイヘンスらの業績の積み重ねの上に、ニュートンが見出した慣性系における運動法則は次の３法則に表現される．

第一法則（慣性の法則）

　外的な力が加わらない限り、物体は静止或いは等速直線運動を続ける．

第二法則（運動法則）

　物体の加速度は、加えた力に比例し、その質量に反比例する．

第三法則（作用・反作用の法則）

　物体が互いに力を及ぼし合うときには、同一直線上で互いに逆向き・同一の大きさの力が働く．

これらの法則は、第一法則で規定される慣性系において（厳密には、我々が住んでいる地表は慣性系ではないが，近似的に適用される。コリオリ力はその現れ。）、加速度 $\boldsymbol a$ [m/s$^2$]、速度 $\boldsymbol v$ [m/s]、慣性質量 $m$ [kg] を用いて、次の運動方程式に要約される．
$$\large{ \boldsymbol a =\frac{\boldsymbol F}{m},}$$ しかし、実用上は、加速度 $\boldsymbol a$ を直接観測する事は無く、速度 $\boldsymbol v$ 或は質点の位置 $\boldsymbol r$ [m] を観測するので、加速度 $\boldsymbol a$ として
$$\large{\boldsymbol a =\frac{d\boldsymbol v}{dt}=\frac{d^2\boldsymbol r}{dt^2}、 }$$ の様に、速度の時間微係数、或は位置座標の時間に関する２階の微係数で表現するのが便利である。
運動の激しさを表す量として「運動量 $m\boldsymbol v$」 が定義される。運動量を用いると、運動方程式は更に単純な形で表現される：
$$\large{ \frac{d\boldsymbol P}{dt}=\boldsymbol F. }$$ 第一法則のように、外力が加わらない場合 $(\boldsymbol F=0)$ は、

$$\large{ m\frac{d\boldsymbol v}{dt}=\frac{d\boldsymbol P}{dt}=0, }$$ $$\large{ \int_{t_0}^{t_1} \frac{d\boldsymbol v}{dt}\,dt=\int_{t_0}^{t_1} d\boldsymbol v=\boldsymbol v(t_1)-\boldsymbol v(t_0)=0, }$$

となり時間が経過しても $t_0$ の時の速度は $t_1$ でも大きさも方向も変化せず、第一法則：外力がないときには速度はゼロまたは一定値を取る、を再現する．しかし、ニュートン以前の常識であった、力が働いていないと運動が保たれない、ことが正しくないことを明確に示すと同時に、運動の本性の重要な性質であることを考えると、第一の法則としての重要性が認められる．

運動量保存則

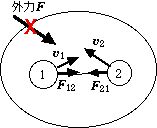
ここで、２つの物体が、衝突して、限られた時間 $\Delta t$ だけ互いに力を及ぼし合う以外に、外的な力が加わらない場合を考えよう．２物体の間には、互いの衝突によって及ぼし合う $\boldsymbol F_{12}$（１から２に及ぼす力）$\boldsymbol F_{21}$（２から１に及ぼす力）（内力）以外の、外部から働く力（外力）は働かないとしよう．衝突前後のそれぞれの物体の運動量を $\boldsymbol P_1$、$\boldsymbol P_2$、および $\boldsymbol P'_1$、$\boldsymbol P'_2$ とすると、衝突の前後で外力が働かない時には、全運動量 $\boldsymbol P=\boldsymbol P_1+\boldsymbol P_2$（衝突前．衝突後はダッシュを付ける）は第三法則（作用反作用、常に $\boldsymbol F_{12}=-\boldsymbol F_{21}$ が成り立つ）を使って、

$$\large{ \frac{d\boldsymbol P}{dt}=\boldsymbol F_{12}+\boldsymbol F_{21}=0, }$$ $$\large{ \therefore\boldsymbol P=\boldsymbol P(t_1)=\boldsymbol P(t_0)=\rm{const.} }$$

が得られる．この関係は粒子数がもっと多くても、外力が働かない限り運動方程式 (1) 式と作用反作用の法則によって成り立つことが保証され、運動量保存則と呼ばれる．とても有用な法則であることは、ジャンボジェット機が空に浮く理由やジェットエンジンで加速できる理由が説明できることからも分かる．

第三法則も、第二法則と惑星の運動の考察から導くことが出来る？

回転せずに等速直線運動、即ち、慣性運動するボールを考える．剛体の運動は、その重心運動がニュートンの運動方程式に従うとしよう．ニュートンの第一或いは第二法則によると、このボールの重心には力が働いていない．このボールの運動方程式は、実際には多くの部分の合成と考えられるので、互いに及ぼし合う内力の和が打ち消していないとすると合力が残るため、その方向に加速される或いは回転運動が起こらなければならない．即ち、慣性運動しない．従って、内力の和が打ち消し合わないという仮定が正しくないと結論される．よって、第三法則：作用・反作用の法則が成り立つ事が要請される．

第二法則は惑星という剛体の運動の解析から導かれているので上記の結論が正しく、第二法則は第三法則を包含しているとも言えるが、ニュートンの第二法則の運動方程式自身が剛体で成り立つことが必ずしも自明とは言えないので、第三法則が独立していることは重要な意味がある．

戻る