２つの質点（大きさがあっても重心の周りの回転運動を考えない、と言う意味で質点）の正面衝突を考える。現実の世界では、必ず衝突をするたびに、２つの質点が持っていた全運動エネルギーは、その一部が、音や熱エネルギーに変化するため、徐々に失われていく。最初は、理想的な場合として、衝突の際に系に含まれる力学的運動エネルギーが全く失われないとしよう。この場合を、弾性衝突、と呼ぶ。

衝突現象は、複数の質点の相互作用を含み、２つのそれぞれの質点についての運動方程式を連立させて解く必要がある。運動方程式は、時間の関数であり、衝突直後のそれぞれの質点の弾性的な歪みをちゃんと取り込んで解かなければならず、一般的に、その解を求めるのは容易ではない。そこで、通常は、衝突前後の状態の間に成り立つ関係式を用いて解くことが多い。そうすれば、衝突中（２つの質点が接している瞬間瞬間）に起こっていることを顕わには考える必要が無くなり、解をずっと容易に求めることが出来る。

さて、弾性衝突の前後で成り立つ２つの関係式は、運動量保存則とエネルギー保存則

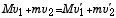	(1: 運動量保存則)
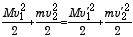	(2: エネルギー保存則)

である。どちらもニュートンの運動法則から導くことが出来る。運動量保存則は、全エネルギーが衝突の前後で保存しないような、非弾性衝突の場合を含む一般的に成り立つ関係式である。弾性衝突の例として、中でも最も単純な場合を考えよう。即ち、２つの質点の質量が等しく、v₂ = 0 の場合である。この場合には、２つの式は

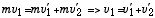	(3)
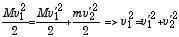	(4)

と書ける。これらの連立方程式は、(3) 式を２乗して (4) 式に代入することにより容易に解ける：
v'₁v'₂ = 0.
この簡単な関係式から、v'₁ = 0 であることが分かる。何故ならば、どちらかがゼロでなければならないことに加えて、v'₂ = 0 だとすると、質点１が、質点２をすり抜けて通過したことになり、現実にはあり得ないためである。結論として、

質点が、静止している同一質量の質点に速度 v で正面衝突すると、持っていた全ての運動量が衝突された質点に移動して、衝突した質点は静止する

ことが分かる。このことは、右図の様な衝突球のおもちゃとして良く知られている。

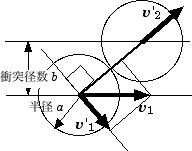図１：２つの摩擦のない同一質量を持つ円盤の衝突。２つの円盤の接点には摩擦力が働かないため、重心を結ぶ方向にしか力が働かない。その方向成分の運動は、(3), (4) 式と同じ解を与えるため、全てのその方向の運動量は、v2' に移動する。それと垂直な速度成分は、衝突によって全く影響を受けないため、v1' の衝突後の速度を与える。

摩擦のない、大きさのある円盤の弾性衝突

次に簡単な例として、摩擦を考えない同一質量の２つの円盤の側面衝突を考える。この時に成り立つ関係式は、(3), (4) 式と同一である。異なる点は、速度が大きさだけのスカラー量ではなく、方向まで持つベクトル量になることである。ベクトル量を太字のアルファベットで表すと、

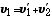	(5)
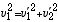	(6)

と書ける。(6) 式で、速度ベクトルの２乗は、速度ベクトルの長さの２乗になることに注意すれば、この連立方程式を解くのも難しくない。(5) 式の両辺を２乗すると、

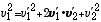(7)

となるので、(6) 式を使って、容易に、

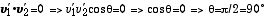(8)

が得られる。ここで、θ は、２つの速度ベクトルが互いに成す角度を表し、

弾性衝突では、図１のように、常に互いに90度の角度を保ちながら衝突後の運動をする。

非弾性衝突

実際の円盤の衝突には、必ず摩擦による力学的運動エネルギーの損失が伴う。その結果として、音が出たり、球の温度が上昇したりする。その効果は、(2) 式の等号が成り立たないとして現れる。即ち、左辺（衝突前）が右辺（衝突後）よりも大きいという不等号で表現される：
．
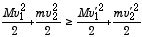この効果は、上の円盤の弾性衝突の例の (6) 式を

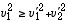
と変化させる。その結果、(8) 式が

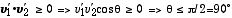
となり、θ が cosθ が１よりも小さい値を与えるような、

θ ≤ π/2 を満たす運動をする。

この結果は、２枚のコインや、浮揚した円盤を相手ゴールに入れるゲームなどで確認することが出来る。