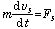戻る

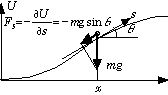
　力学的全エネルギーの保存則を満たすような力を保存力と呼ぶ．それはどの様な力か調べてみよう．簡単のために、ニュートンの運動方程式の s 成分（運動する道筋の接線方向成分、下の図を参照）、

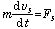(1)

を考えよう．(1) 式を s について積分すると運動エネルギーの変化分と、為された仕事量の関係が得られる：

、

、

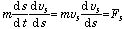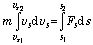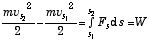． (2)

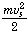は運動エネルギー、そして、 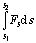は外力 F_s がその物体を位置 s₁ から s₂ まで移動させる間に物体に為した仕事量 W である。すなわち、外力がした仕事 W が、運動エネルギーに変わった事を示し、力学的全エネルギーの保存則が成立つことに対応している．この時に、系や場（地表であれば「重力場」、バネ、電磁気的力であれば「電場」、「磁場」など）に内在するエネルギー U （すなわち、ポテンシャルエネルギー）が、物体に仕事をする場合を考えると、W = U(s₁) - U(s₂) =- (U(s₂) - U(s₁)) と書ける：

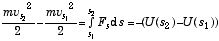． (3)

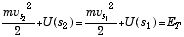． (4)

ここで、 E_T は力学的全エネルギーで、この運動の保存量を表している。このように、ポテンシャルエネルギーの勾配に起因する力が働く場合にはエネルギー保存則が成り立ち、その場合の力を保存力と呼ぶ。(3) 式の第２辺と３辺で s₂-s₁=Δs （微少量なので、F_s はその間で一定として良い）と置きゼロの極限を取れば、保存力を

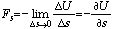、 (5)

と書くことが出来る．U の例としては、重力場、バネ、電場、磁場などによるポテンシャルエネルギーがある．

　地表の重力場 U(h)=mgh(s) の例で考えると、山や谷の凹凸が重力場の依存性を表す．(5) 式から、我々の体験から良く知られている形、山の傾斜 sinθ に比例した力、

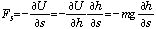=-mgsinθ、

を傾斜の-s の方向に受けることが出てくる．

# 16/6/04改訂

戻る