HOME 物性物理学 II・コメント Dpt. Phys. TMU

戻る
同じ情報が http://spinman.phys.se.tmu.ac.jp/Lecture/CMPComH24.html と
http://kem3.com/ESRP/Lecture/CMPComH24.html に置いてあります。
物性物理学 II・H24 （後期　シラバス）
＜プリント＞
  • cgs単位系のクーロン相互作用
    		•
  • cgs-SI 単位変換表
    		•
  • 原子の磁性
    		•
  • ブリルアン関数
    		•
  • 固体中の磁性
    		•
  • 金属のLandau反磁性（S. Teitel, Univ. of Rochester）
    		•
  • 磁気秩序(11/6修正版)
    		•
  • 誘電応答(12/4改訂版)
    		•
  • 半導体(11/25修正版)
    		•
  • 超伝導1
    		•
  • 超伝導2(1/9修正)
    		•
  • Spatial Structure of the Cooper Pair（A. M. Kadin, Princeton.edu）
    		•
  • Superfluidity
    		•

    ○　本日で終了しました。本日の超流動関連のレポートは最終レポートと一緒に提出して下さい。
    〆切は、２月１日（金）とします。提出は、メール添付の電子ファイル (pdf 推奨) でも良いです。

    １）　体積が１cm3 の液体ヘリウムにおいて、基底状態の次の、最初の励起状態のエネルギー (ε1(nx=1, ny=nz=0)) を計算して下さい。SI 単位系で、単位はエネルギー [J] と温度 [K] の両方で示して下さい。この量は、λ点（2.17 K) より遥かに超低温であり、近似的に励起状態は連続と考えて差し支えない。この点が、エネルギーギャップを持つ超伝導転移とは本質的に異なる。

    ２）　液体ヘリウムの温度を下げていき、温度 T0 になると基底状態を除いた励起状態の全状態数が、粒子数 N (≈ 2.2 × 1022 個/cm3）よりも小さくなり、それ以下の温度ではマクロな数の粒子が基底状態を占める様になる。これが超流動の原因になる。T0 の大きさ（表式はプリント参照の事）を見積もって下さい。

    　最終レポートは、各自の修論、卒論のテーマで最も重要と思われる論文（短いのでOK）の解説を提出して下さい。

    ○　明けましておめでとうございます。今年度も残り少なくなってきました。
    フォノンを媒介とした超伝導はBCS理論で理解された訳ですが、現象論的な理解（解った様な気にさせる？）を助ける説明が早大の栗原進さんのサイト（左メニュー「超伝導とは」）で見掛けました。関心のある人は訪ねてみて下さい。
    ○　12/12提出のレポートについて

    １）３次元の自由電子金属（有効質量m*）の状態密度 D(E) を求めて下さい。

    ２）エネルギーギャップが Eg の半導体において、温度 T における伝導電子バンドの電荷担体数 nc を、１）で求めた状態密度 D(E) と高温近似したフェルミ分布関数 ƒ(E) を用いて計算して下さい。
    nc = ∫Ec∞ D(E)ƒ(E) dE

    ○　誘電応答のプリントを改訂しました。(12/4)
    ○　12/5提出のレポートについて

    Maxwell方程式から、真空中の電磁波の運動方程式を導出してください。
    ∂2E/∂t2 = (1/μ0ε0)∇2E

    ○　11/28提出のレポートについて：プリントに議論していますが、以下の点をレポートしてください。

    1）分極 P [C/m2] が表面電荷密度に等しい事を自分の考えで検討してください。

    2）正負の電荷 q、-q をそれぞれ x-軸上の a、-a に置いた電気双極子モーメントの作る静電ポテンシャル φ(r) を求めなさい。

    3）E = -∇φ より、電気双極子モーメントの作る電場を求めなさい。

    ○　11/14提出のレポートについて

    １）強磁性転移温度 TC が約 1,000 K の Fe について、最近接スピン数 z = 8、スピン S = 1/2 として、交換相互作用エネルギー J を求めて下さい。その際に、単位として、[J] と [eV] の両方で出して下さい。

    ２）授業中には説明し忘れましたが、プリントの６ページ目にある課題の３）も計算して下さい。
    ＜Sz＞ = 1/2 として、各スピンが受ける分子場
    BE = 2zJ＜Sz＞/gμB
    を、単位を明記の上、求めて下さい。

    ○　本日の最後の板書に間違いがありましたので、プリントの７頁 (12) 式以降に従って訂正をお願いします。
    （(13)式で、BEa,b を Bsa,b と誤記。(14)式の第３辺で、(λ1 - λ2) 分の１を書き落とし。）

    ○　反強磁性体の同一副格子内の（次近接）スピン間に働く分子場係数を
    BEa,b = - λ2M, |λ2| > 0 とした点の注です：
    次近接スピン間にも反強磁性的な相互作用が働くが、最近接スピン間のより強い反強磁性的相互作用のために、次近接スピン間は互いに平行になっている、という状況を表しています。
    従って、次近接スピン間の反強磁性的相互作用は、最近接スピン間の反強磁性的相互作用を部分的に打ち消して TN を押し下げる役割をしていることになります。

    ○　本日提出してもらったレポートで、スピン数 N として具体的な数値を見積もっていないケースが多いです。これを見積もらないと、温度として、TC = 1,000 K との関係がつかめません。Fe について、その密度と原子量から単位体積あたりのスピン数を見積もってみて下さい。1029 [m-3] 程度になるはずです。その結果、1 K よりかなり低い転移温度が出てきます。

    ○　11/7提出のレポートについて。

    　Weiss の分子場近似による強磁性転移温度 TC（11/7に導出します）は、
    BE = λM 　(λ [H/m=Wb/Am]、cgs では無次元)　　　　(A)
    で定義される分子場係数 λ を用いて
    TC = Ng2μB2S(S+1)λ/3kB 　　　　　(B)
    で与えられます。ここで、M は単位体積あたりの強磁性体の自発磁化、BE は、ある注目する磁気モーメントの位置に周囲の全ての磁気モーメントが作る磁場の和である有効磁場を表します。有効磁場が、強磁性体の自発磁化に比例するというのは自然な仮定でしょう。
    　また、誘電体で考察されたLorentzの局所場の考え方から（11/14に導出予定）、双極子モーメントからなる等方的な磁性体中の有効磁場は
    BE = B0 + (μ0/3)M 　(cgs では H + (4π/3)M)
    で与えられます。強磁性体の自発磁化を考える場合は外部磁場 B0 = 0 なので、(A)式との比較から λ= μ0/3 が得られます。これを(B)式に代入して、電子スピンの磁気双極子モーメントによって起こりうる強磁性転移温度を、単位に注意して、見積もって下さい。

    ○　10/24提出のレポートについて。（10/31は大学祭で休講です）

    １）ベクトルポテンシャル A = (B × r)/2
    の発散が
    rotA = ∇ × A = B
    を満たす事を確認しなさい。
    （注：∇は微分演算子なので、通常のベクトル三重積の展開則では表せません。関数の積の微分演算に相当します。例：(∇•A)B = (∇A•A)B + (A•∇B)B：∇i は、 i ベクトルのみを微分する意）

    ２）He と Xe の反磁性磁化率が以下の様に与えられた時、電子軌道の平均的な広がり (<r2>)1/2 を求めなさい。この量は、その原子の平均的な電子軌道半径の目安を与えます。
    χdia, cgsHe = –1.9 × 10-6 (emu/mol)
    χdia, cgsXe = – 48 × 10-6 (emu/mol)
    cgs-Gauss単位系では、SI系の式中の、e を e/c で置き換えた形をとります：
    χdia, cgs = (NAZe2/6mc2)<r2> (emu/mol)
    ここで、NA はアボガドロ数、Z は原子内の全電子数で、全て cgs 単位系の量を代入します。

    ○　10/17(水)提出レポートについて。

    １）N 個の磁気モーメント μJ = gμBJ の系を考える。このスピン系の、温度 T、磁場（磁束密度 B）中における分配関数 Z が以下の式で与えられる事を示しなさい。


    ２）磁化の熱平均値が、Brillouin関数で表される事を分配関数を用いて示しなさい。
    ここで，M = -∂F/∂B = kBT ∂(lnZ)/∂B を用いる。

    　Brillouin関数のグラフを書いてみましょう。JBJ(a) を、a = μJB/kBT と、a として b = μBB/kBT の２つの場合の違いを考えてみましょう。


    ○　10/3(水) の10/10(水) 提出レポートについて。

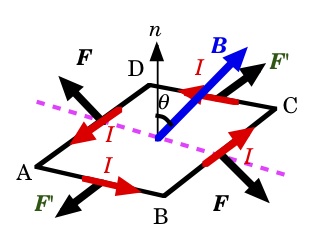
    １）電流ループの作る磁気双極子モーメントが以下の様に表される事を，右図に示す正方形の閉電流が磁場から受けるトルク(力のモーメント)を計算する事により示しなさい。（不明な点はメールで質問して下さい）
    μEB = SI 　(SI単位系，E-B）
    μcgsG = SI/c 　(cgs-Gauss)
    E = -μ•B = -μBcosθ より，磁場中の磁気モーメントに働くトルク Nμ = -dE/dθ を計算し，右図の閉電流に働くローレンツ力によるトルク NI と等しいとして，閉電流の磁気モーメントの大きさ μI を求めなさい。cgs-G 系では，ローレンツ力に1/c の係数が掛かる事に注意して下さい。(赤字部分，訂正です。混乱させ陳謝！)

    ２）ボーア磁子(Bohr magneton)の具体的な数値を求めなさい。用いる物理量の単位を統一して明記の上計算して下さい。ℏ も me も，それぞれの単位系で表した数値を使います。
    μBSI = eℏ/2me 　 [Kg, m, s]
    μBcgsG = ecgsGℏ/2mec 　[g, cm, s]

    興味のある人は，cgs-Gのクーロンの法則と，SI のクーロンの法則の比較から（例えば，r = 1 [m] = 100 [cm])，esgsG と eSI の間の関係を考えてみて下さい。（参考サイト）
    FcgsG [dyn] = esgsGesgsG [esu2] /r2 [cm2]
    FSI [N] = eSIeSI [C2] /4πε0r2 [m2]

    ○　講義は板書を主体に進める予定です。参考書としては、

    1. Introduction to Solid State Physics：Charles Kittel：John Wiley & Sons, Inc.
    2. 訳本：固体物理学入門：チャールズ・キッテル著：岩波書店
    3. 物性論 -固体を中心とした-：黒沢達美：裳華房・基礎物理学選書９（易）
    等がお勧めです。