|
◎ 半年間、お疲れ様でした。今後も、力学で気になることがありましたら、何時でもメールをお寄せください。相談に乗ります。
◎ 7/19 本日の授業内容(惑星の運動)からは、以下のようなキーワードで期末テストで問う予定ですので、見直しておいてください。
- 中心力場中の惑星の運動：惑星の運動（中心力場中の運動）において、太陽から測った惑星の位置ベクトル $\vec{r}$ と万有引力 $F_{万}=-\large\frac{GMm}{r^2}\hat{r}$（$\hat{r}$ は $r$ 方向の単位ベクトル）が常に平行なため、惑星に働く万有引力による「力のモーメント」は常にゼロになる：$\vec{N}=\vec{r}\times\vec{F_{万}}=0$。
$\large\frac{d\vec{L}}{dt}$$=\vec{N}=0$ より、角運動量保存則が成り立つので、公転運動をする惑星の持つ角運動量 $\vec{L}$ は時間に依らず常に一定である。
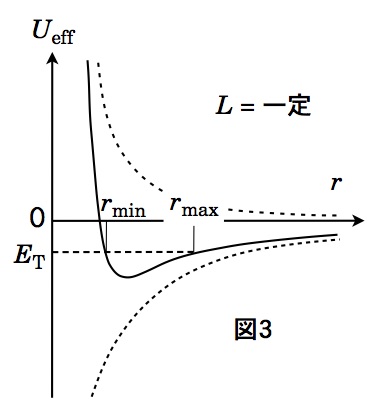
- 有効ポテンシャル：一般的にはポテンシャルエネルギーは太陽による万有引力ポテンシャルのみであるが、1. より定数である「惑星の持つ角運動量 $\vec{L}$」の２乗に比例する「遠心力の大きさ $mr\omega^2=\large\frac{L^2}{mr^3}$」も公転運動中は位置 $r$ にのみ依存する。そのような力はポテンシャルの偏微係数 $F=-\large\frac{\partial U}{\partial r}$ で表され、「保存力」と呼ばれる。
そこで、万有引力と遠心力をそれぞれ太陽の中心から惑星の位置まで $r$ について積分して（保存力の式より $U=-\int_0^r Fdr$）得られる「万有引力ポテンシャルと遠心力ポテンシャル」の２つを加え合わせた $U_{eff}=-\large\frac{GMm}{r}+\frac{L^2}{2mr^2}$ を有効ポテンシャルと呼ぶ。
惑星や人工衛星の持つ全力学的エネルギー $E_T$ が分かると、有効ポテンシャルの動径距離依存性のグラフからどのような軌道運動をするかを考察することができる。例えば、有効ポテンシャルが最小値をとる動径半径では、両ポテンシャルの微係数（傾斜が保存力の大きさになる）が丁度等しく、遠心力と万有引力とが吊り合う位置に相当し、半径が一定の円運動を表す。
また、星の密度が非常に高い原子核のみからできている中性子星の場合は、光速で走る光でさえ万有引力に逆らえずに取り込まれてしまう。これは古典的なブラックホールを表す。
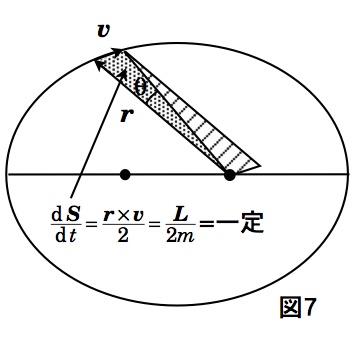
- ケプラーの第二法則：面積速度一定の法則。惑星の位置ベクトルが惑星の軌道運動とともに単位時間あたりに掃過する面積 $S$ は一定である。
半径ベクトル $\vec{r}$ と速度ベクトル $\vec{v}$ が作る平行四辺形の面積 $2S$ の時間変化率 $\large\frac{d(2S)}{dt}$ は２つのベクトルの外積の大きさに等しいので、惑星の面積速度は、$\large\frac{dS}{dt}\normalsize=\large\frac{|\vec{r}\times\vec{v}|}{2}\normalsize=\large\frac{L}{2m}$=一定、となり、常に一定である。
- ケプラーの第三法則：惑星の公転周期 $T$ の２乗と軌道の長軸半径 $a$ の３乗の比は全ての惑星について等しい。
簡単な例として円軌道を考えると、万有引力と遠心力が吊り合うことが条件になる：$\large\frac{GMm}{a^2}$$=ma\omega^2$
$\omega=2\pi/T$ を代入して整理すると $\large\frac{a^3}{T^2}$$=\large\frac{GM}{4\pi^2}$＝一定が示される。
- 地表の高度を回る人工衛星に必要な速度を第一宇宙速度と呼ぶ。この場合の万有引力は「地球による」地表に於ける万有引力（重力、$mg$）であり、人工衛星に働く遠心力が重力 $mg$ と吊り合う場合に相当する。第一宇宙速度を求めなさい。
参考：他の惑星に向けて飛び立つためには地球の重力圏を脱出するので、全力学的エネルギー $E_T=\large\frac{mv^2}{2}-\frac{GMm}{r}$ が正になるような運動エネルギーを持つ必要がある。この場合は地球の周回軌道ではないため有効ポテンシャルは使わず、人工衛星の運動エネルギーと万有引力ポテンシャルを用いて考える。従って、速度の方向は地球に衝突しない限り、どちらを向いていても構わない。この場合の人工衛星の速度を「第二宇宙速度」と呼ぶ。
◎ 7/26 は期末テストです。テスト範囲は、以下の通りです。
- ニュートンの運動法則の理解
- 単振動
- エネルギー保存則、保存力、衝突（エネルギー＆運動量保存則）
- 回転運動の運動方程式、力のモーメント、角運動量保存則
- 惑星に関するケプラーの法則と、そのニュートンの運動法則による説明（面積速度一定（第二法則）、軌道半径と周期（第三法則））
◎ 残りの２回の授業で、「惑星の運動」のニュートンの運動法則による再現を試みます。(7/10)
そのためには、前回、向心力を見かけ上消去することによって得た、運動方程式を解かなくても外力が回転体の運動に及ぼす影響の予想を可能にしてくれる「回転の運動方程式」$\large\frac{d\vec{L}}{dt}$$=\vec{N},\ $と $\vec{L}=\vec{r}\times\vec{P},\ $(N•m•s=kg•m$^2$•s$^{-1}$) $\vec{N}=\vec{r}\times\vec{F}$ (N•m=kg•m$^2$•s$^{-2}$) が大事な式になります。
角運動量 $\vec{L}$ は回転運動の激しさを、力のモーメント $\vec{N}$ は回転運動を起こす能力を表します。
回転の運動方程式から言えることは、回転させる能力の「力のモーメント」が働かない $\vec{N}=0$ の場合は、回転の激しさの「角運動量 $\vec{L}$」が一定に保たれることです。この大事な回転運動の不変性を「角運動量保存則」と呼びます。
一方、常に向心力を受けながら公転運動をする惑星の解析には、回転する座標系に乗った場合に現れる「見かけの力」である遠心力を「有効（遠心力）ポテンシャル」としてあらわに取り込んで、惑星を中心とした運動方程式に変換して解析を進めます。
◎ エネルギー保存則の確認レポートについて、解答例を整理しました。
- まず、一般的に、重力場中の力学的エネルギー保存則について。
任意の向きの速度を保つ質点の運動エネルギーと位置エネルギーの和は摩擦が無い場合には、常に一定です。
$$m\int_{\vec{r}_1}^{\vec{r}_2}\frac{d\vec{v}}{dt}\cdot d\vec{r}=m\int_{\vec{v}_1}^{\vec{v}_2}\vec{v}\cdot d\vec{v}=\frac{mv_2^2}{2}-\frac{mv_1^2}{2}$$
$$=m\int_{\vec{r}_1}^{\vec{r}_2}\vec{g}\cdot d\vec{r}=-m\int_{z_1}^{z_2}gdz=-mgz_2+mgz_1$$
左辺に「2」を、右辺に「1」をまとめると、
$$\frac{mv_2^2}{2}+mgz_2=\frac{mv_1^2}{2}+mgz_1=\rm{const.}$$
のように、2つの位置 $\vec{r_1},\ \vec{r_2}$ において、運動エネルギーと位置エネルギーの和の力学的エネルギーが変化しません。この2つの位置は任意の位置を表していますので、どこに運動しても力学的エネルギーが保存されることを表しています。定積分の代わりに不定積分にすると、力学的エネルギーが（積分）定数に等しい、となります。
- 一方、成分に分けて積分した場合は、
$$m\int_{x_1}^{x_2}\frac{dv_x}{dt}dx=m\int_{x_1}^{x_2}v_xdv_x=\frac{mv_{x2}^2}{2}-\frac{mv_{x1}^2}{2}=0,\ \therefore \frac{mv_{x2}^2}{2}=\frac{mv_{x1}^2}{2}$$
$$m\int_{y_1}^{y_2}\frac{dv_y}{dt}dy=\frac{mv_{y2}^2}{2}-\frac{mv_{y1}^2}{2}=0$$
$$m\int_{z_1}^{z_2}\frac{dv_z}{dt}dz=\frac{mv_{z2}^2}{2}-\frac{mv_{z1}^2}{2}=-mg\int_{z_1}^{z_2}dz=-mgz_2-mgz_1, \ \therefore \frac{mv_{z2}^2}{2}+mgz_2=\frac{mv_{z1}^2}{2}+mgz_1$$
$x,\ y$ 成分は、1から2に移動しても、$x,\ y$ 方向に外力が働かないので重力場による仕事はされず、運動エネルギーが保存されることを表します。$z$ 方向は重力によって速度と位置エネルギーが変化しますが、1と2を両辺に分けて考えれば、力学的エネルギーの和が変化しないことを示しています。
◎ 期末テストは 7/26 に予定しています。シラバスには 8/2 となっていましたが、訂正しました。
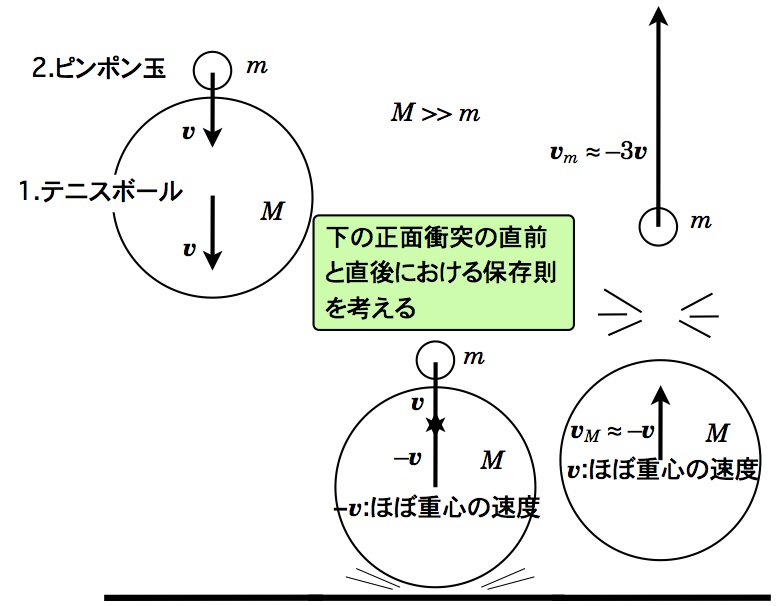◎ 7/12 提出のレポートは、親子ボールです。質量 M の重い親ボールの上に質量 m の軽い子ボールを載せて自由落下させます。地表で衝突して跳ね返りますが、子ボールは単独で弾ませた場合よりも遥かに高く上がります。右図の中央が、親ボールが床と衝突した直後を表しています。
- 静止している床に速度 $v$ で衝突した後の親ボールの速度 $v_M$ を求めて下さい。
エ：$\large\frac{Mv^2}{2}=\frac{Mv_M^2}{2}+\frac{M_E v_E^2}{2}$
運：$Mv=Mv_M+M_E v_E$
これらの保存則を連立させて解き、$M_E\gg M$ の極限を取り $v_M=-v$ を確認します。ここで、$M_E,\ v_E$ は地球の質量と速度です。
- （１）の直後に、速度 $-v$ の親ボールと速度 $v$ の子ボールが正面衝突します。正面衝突前後のエネルギーと運動量の両保存則を連立させて解き、正面衝突直後の子ボールの速度 $v_m$ を衝突前の速度 $v$ で表します。次に、求めた解を $M\gg m$ で近似して $v_m\simeq -3v$ であることを確認してください。
- 子ボールが単独に速度 $v$ で床と衝突後に跳ね上がる高さと比較して何倍まで跳ね上がるか見積もります。
なおこの例題は、$M\gg m$ より親ボールの重心に親子ボールの重心があり、正面衝突前の重心の速度は $v$ なので、正面衝突を、重心に乗って（重心系で）親子ボール間の相対速度で考え直すと比較的容易に $v_m\simeq -3v$ が予想できます。
◎ 直しレポートは、60点以下の場合のみ考慮しますので、それ以上の得点の場合は結果には反映されません。
◎ 相変わらず、ベクトル表記をしないでベクトルの積りで使っている答案を見かけます。期末テストでは、ベクトルをベクトル表記していない場合は「X」としますので、留意してベクトル表記をする癖をつけてください。
◎ 6/28 提出のレポートチェックの結果について：実験の準備をする上で便利なように、振り子の長さを約1mとしました。レポートを見ますと、長さを明記していなかったり、「1 m」と有効桁数を1桁しか示していないレポートが大半でした。少なくとも1cmの精度で計れるはずですし、時間も$T_0$ を十分の1秒以下の精度では計れるはずです。また、長さと時間の有効桁数を1桁としておきながら、重力加速度を3桁も4桁も表示するのは実験を解析する上で避けなければいけない点です。
◎ 7/5 提出のレポートは、地表面の重力場における力学的エネルギー保存則の確認です。
- 地表における重力場中の質点の運動方程式
$$m\frac{d\vec{v}}{dt}\normalsize=m\vec{g}$$
の両辺を $\vec{r}$ で積分する。ここで鉛直上方を $z$-軸に取り、重力加速度ベクトルを $\vec{g}=(0,0,-g)$ とする。
- $$m\int_{\vec{r}_1}^{\vec{r}_2}\frac{d\vec{v}}{dt}\cdot d\vec{r}=m\int_{\vec{v}_1}^{\vec{v}_2}\vec{v}\cdot d\vec{v}=m\int_{\vec{r}_1}^{\vec{r}_2}\vec{g}\cdot d\vec{r}$$
上式を成分に分けて両辺を積分して運動エネルギーと位置エネルギーの合計に対して力学的エネルギー保存則 $\large\bigl(\frac{mv_z^2}{2}\normalsize+mgz=$const.: 力学的エネルギー保存則としては自由落下にしか適応せず不適当でした$\bigr)$ $\large\frac{mv^2}{2}\normalsize+mgz=$const.が成り立つことを確認する。
◎ 6/28 提出のレポートでは、振子の周期から重力加速度を求めてください。
- 長さ $l$ が 1m 程度の糸に錘を付けて吊るし、10 回分の振動に要する時間 $t_{10}$ から振子の振動周期 $T_0$ を求める。
- $T_0=2\pi\sqrt{\large{\frac{l}{g}}}$ に代入して重力加速度 $g$ を求める。全ての物理量には単位を必ず付けること。
◎ 中間テストは如何でしたか。採点後に返却をしますので、直しレポートを提出したい学生さんは、返却された答案の赤字を理解した上でレポートの作成をしてください。
後半の授業は単振動から入ります。
◎ 摩擦のある自由落下のレポート：雨粒で、1,000 m から降る場合は、約140 m/s になります。
一方、粘性抵抗の場合は、終速度のみを計算してもらいました。粘性抵抗は非常に小さいため、1,000 m では全く終速度には到達しませんので、粘性抵抗の場合の終速度は、1,000 m からの自由落下より遥かに高速になります（Y君、間違っていませんよ、ただし、単位を kg, m に直して計算すれば）。（訂正：1,000 m 以内に終速度に達するようです、時速400 km/h 以上ですが。）
しかし、慣性抵抗は粘性抵抗よりも遥かに大きく、自由落下開始後に直ちに終速度に到達しますので、抵抗なしの 1,000 m からの自由落下よりも遥かに遅く、秒速 約数 m/s と、現実の世界と同じ程度になります。
数値的な結果を導く際には、代入する物理量に単位を付して式の前に整理するようにしてください。又、それらを代入する式を書いた上で代入してください。何が、どんな式に代入されたのか判断に苦しむレポートが続出しています。
例：$m$=60 kg, $g$=10 m/s$^2$, $a$=2.5 m, $\eta$=1.8x10$^{-5}$ Pa•s とすると、粘性抵抗のみの場合の終速度は、
$$v_{vf}=\frac{mg}{6\pi a\eta}=\frac{60\times10}{6\times3.14\times2.5\times1.8\times10^{-5}}=\ ...\ \rm{m/s}$$
高校で憶えた公式用の式は、必ず用いる記号を定義の上、ニュートンの運動方程式から導出してから用いること。例：
$v^2-v_0^2=2ax$ など。
ニュートンの運動法則の理解につながらないので、大きく減点します。
◎ 6/14 に中間テストを予定しています。内容は、ニュートンの運動方程式を始め、授業で出てきた例題が中心になります。
- ニュートンの運動の３法則とその説明。運動量保存則。（ニュートンの運動法則のプリント参照）
- 地表における質点の運動：運動方程式、一般解、問題で与えられた条件の特解。（質点の運動のプリント参照）
- 斜面上の質点の運動。（斜面上の質点の運動のプリント参照）
- 空気抵抗がある場合の運動方程式（空気抵抗の導出法は問いません）。（空気抵抗のプリント参照）
- 風（空気）の運動量と風から受ける力。（竜巻・風の力のプリント参照）
◎ 6/7 提出のレポートは、雨粒とパラシュートを想定して、空気抵抗の自由落下速度への影響を調べます。空気の密度は $\rho=1.3$ kg/m$^3$、重力加速度は $g=10$ m/s$^2$ とします。
- 雨粒の自由落下：直径が 2 mm の球形とします。その質量は、球の体積と水の密度 1 g/cm$^3$ から求めます（式に代入する時には単位を必ず kg, m, s に統一すること）。求める速度は、
- 高度 1,000 m からの自由落下の地表における落下速度 $v_{ff}$。自由落下の運動方程式の解を利用して、地表まで落下に要する時間から、その時の速度を求める。
- 粘性抵抗 ($F_v=Cv$, viscos drag) のみが働くとした場合の雨粒の終速度：$v_{vf}=\frac{mg}{C},\ \ C=6\pi a\eta$、$a$ は雨粒の半径、$\eta$ は空気の粘性係数。
- 慣性抵抗 ($F_i=Dv^2$, inertial resistance) のみが働くとした場合の雨粒の終速度：$v_{if}=\sqrt{\frac{mg}{D}},\ \ D=S\rho$、$S$ は雨粒の断面積、$\rho$ は空気の密度。
各自、運動方程式から終速度を導く過程を確認しておくこと。
- 直径が 5 m のパラシュートの終速度を調べる。質量は各自の想定体重とする。
- 粘性抵抗のみが働くとした場合の終速度。粘性抵抗の係数 $C$ の半径 $a$ は、パラシュートの半径を用いる。
- 慣性抵抗のみが働くとした場合の終速度。
- 得られた雨粒の終速度の中で、どれが最も現実の雨粒の落下速度に近いかを考察する（雨粒の落下の様子は目視で確認できると思います。電車の窓ガラスに残る雨の跡の角度と電車の速度（時速 100 km/h 前後)）から大まかな数値を見積もる事も出来ます）
- 得られたパラシュートの終速度で、無事に地表に降り立つことが出来るかどうか、考察する。
◎ レポートの「2.」の意図を正しく汲めなかった学生さんが多くいました。「... $x_{max}$ を使って示しなさい。」を「... $x_{max}$ を示しなさい」と読み誤ったようです。
◎ 空気抵抗は現実を理解するためには不可欠です。風から受ける力も空気抵抗が原因です。
◎ 5/24 のレポートは以下の通りです。
- 原点から $x$ 軸に対して角度 $\theta_0$、初速度 $\vec{v_0}=(v_{0x},v_{0y})$ で質点を投げ上げた場合の運動についてニュートンの運動方程式を解きました。得られた時刻 $t$ における $x=v_{0x}t$ 及び $y=-\frac{1}{2}gt^2+v_{0y}t$ から時間 $t$ を消去して、質点の高さ $y$ を水平位置 $x$ の関数として求めなさい。
- 質点の運動のプリントの2ページ目最後にある問１の前半部分：同じ初速度で最も遠くまで投げるためには角度 $\theta_0$ を45度にする必要があります。前問の結果を用い、落下地点では質点の高度が $y=0$ となることを利用して得られる到達距離 $x_{max}$ を使って示しなさい。
(iOSのSafariでプリントのリンクを直接開くと最初のページしか表示されません。2ページ目以降も表示するには、リンクの長押し=>新規タブで開く、を選択してください。)
- プリントの問2。$x_{max}=100\ \rm{m}$ を得るために必要な初速度の大きさ $v_0$ を求めなさい。その際に、投げ上げ角度 $\theta_0$ は各自の誕生月に 0 を追加してください（例：5月：50度）。なお、9月以降はその角度から80度を差し引いてください（例：11月：110-80=30度）。なお、初速度は平方根や分数を開き、有効数字２桁で表すこと。空気抵抗は考慮していませんが、現実的な初速度かどうかを確認してください。
◎ 5/17 のレポートはありません。ニュートンの運動法則のプリントを微修正しました。左ページの最後の式が不適当でしたので訂正しました。
◎ 「ニュートンの運動の3法則」はテストの度に出題しますので、十分理解しておいてください。疑問点は何時でもメール下さい。
授業の最後に見てもらった動画は、1）身近な物体の運動を考える際に、この授業の結果を考える時にその重心を考えれば良いこと、2）力が加わる方向の運動のみが変化し、力と垂直な方向の運動は変化しない（力の影響を受けない）ことを伝えていました。2）は、ニュートンの運動方程式 $\frac{d\vec{v}}{dt}=\vec{F}$ の予測と一致します。1）は、初等物理 II で学ぶと思います。
◎ 5/10 提出のレポートは、ベクトルのプリントの２枚目の左側の問１）、２）です。
１）は、３つのベクトル $\vec{A}=A_x\vec{i}+A_y\vec{j}+A_z\vec{k},\ \vec{B}=B_x\vec{i}+B_y\vec{j}+B_z\vec{k},\ \vec{C}=C_x\vec{i}+C_y\vec{j}+C_z\vec{k}$の下に示す外積（左辺）を $x,\ y,\ z$ 方向の単位ベクトル $\vec{i},\ \vec{j},\ \vec{k}$ で展開して整理し、右辺と等価であることを示してください。
$$\vec{A}\times(\vec{B}\times\vec{C})=\vec{B}(\vec{A}\cdot\vec{C})-\vec{C}(\vec{A}\cdot\vec{B})$$
(ヒント）多くの学生さんは既に証明できていると思います。未だ解けていない学生さんにヒントです。上式の $x$ 成分(単位ベクトル $\vec{i}$ の係数)だけを書いてみると分かりやすいでしょう。左辺は以下のようになります。
$$\{\vec{A}\times(\vec{B}\times\vec{C})\}_x=A_y(\vec{B}\times\vec{C})_z-A_z(\vec{B}\times\vec{C})_y=A_yB_xC_y-A_yB_yC_x-A_zB_zC_x+A_zB_xC_z$$
右辺のカッコ内は2つのベクトルの「内積」ですから、成分が1つのみのスカラー量になります。ベクトルとして残っているのは、$\vec{B}$ と $\vec{C}$ だけです。したがって、右辺の $x$ 成分は、
$B_x(\vec{A}\cdot\vec{C})-C_x(\vec{A}\cdot\vec{B})$
となります。これらの内積の成分を書き下し、左辺の $x$ 成分と見比べれば等価性が見えてきますよね。
２）は、プリントの１枚目の右側２つめの図を参照し、ベクトル $\vec{a},\ \vec{b}$ の内積の定義 $\vec{a}\cdot\vec{b}=ab\cos\theta\ (=ab\cos(\alpha+\beta))$ と $\vec{i},\ \vec{j},\ \vec{k}$ 成分で表した内積を利用して
$$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$$
を示してください。
◎ 4/19 提出のレポートとして、これまでの皆さんの知識を元に、授業の最後に見たビデオについての感想をA4用紙１枚程度にまとめてください。ニュートンの運動3法則のビデオ(ここにあります)
◎ このページに適宜、レポート内容、解説、コメントなどを載せていきますので、定期的に見るようにしてください。
○ レポートの書き方
○ 講義はここでアップするプリントを元に、板書を主体に進める予定です。参考書としては、
- 基礎物理学（第3版、第4版）：原 康夫著：学術図書出版社（物理全般、易）
- 物理学：原 康夫著：学術図書出版社（物理全般、中）
等がお勧めです。教科書代わりには、１が良いでしょう。
|