| HOME | 物性物理学 II・コメント | Dpt. Phys. TMU |
| 同じ情報が http://spinman.phys.se.tmu.ac.jp/Lecture/CMPComH21.html と http://kem3.com/esrp/Lecture/CMPComH21.html に置いてあります。 |
| 物性物理学 II・H21 (後期 シラバス) | |||||||||||||||||||||||
| |||||||||||||||||||||||
|
○ 超伝導の簡単なプリントをアップしました。超伝導に関する参考書としては、「超伝導現象」M. ティンカム著(小林俊一訳)産業図書株が実験屋さんには読みやすいです。
○ 12/2 提出のレポートは、プリント「磁気秩序」6ページの問3題です(途中に10ページが入っていますが御容赦を・・・)。
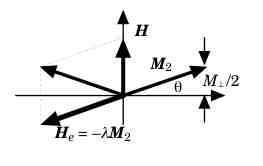
○ 11/25もレポートは無しです。 11/18の講義の最後に紹介した反強磁性体の転移温度以下における磁化率の内、χ⊥ に付いてのコメントです。右図に示すように、χ⊥ は、反強磁性の自発磁化の方向と垂直に磁場を掛けた場合に、自発磁化がどの様に傾くかによって決まります。磁化M2 が磁化 M1 の位置に作る分子場 He は、水平軸に対して -θ(縦軸負の方向)傾いています。従って、分子場との合成ベクトル H' = H + He の方向は、+θ方向(縦軸正の方向)で、M1 と平行になります。その時の角度θは、 ○ 11/18提出のレポートはありません。
○ 10/27提出のレポートについて:μH/kBT の関数としてBrillouin関数を皆さんに書いてもらいました。その図を見ていて「何かおかしい!?」と感じたのですが、その理由は、S=5/2 の場合の方が S=1/2 の場合よりも立ち上がりがずっと遅かったからです(右上図)。理由は、BS を μH/kBT に付いて書いたからで、M ∝ SBS(μBH/kBT) にすれば、よく見る右下図になりました。この図の横軸は、温度を一定にして測定したときに、どのスピンの場合も、同じ磁場を掛けて比較したことになります。即ち、T = 1 K の時に、b の数字がほぼテスラ(T)程度のオーダーになります。(a と b が板書と反対になりました。すいません)(11/4) ○ 次回は、11/3は教室が使用できないことと、学部生も受講しているので、大学祭の後の11月11日になります。レポートも11/4では無く、11/11に提出になります。 ○ ブリルアン関数のプリントをアップしました(10/28)。始めから a = μH/kBT = gJμBH/kBT で統一して整理しました。 ○ 11/4提出のレポートです。
○ スピン軌道相互作用のプリントを修正しました(10/25)。 ○ 10/27提出のレポートです。
○ 10/21提出のレポートは、3d遷移元素のd-電子の表を埋める問題です。前回のレポートの説明プリントをアップしました。
○ 明日10/14提出のレポートは、数値を代入する計算例です。
○ 講義は板書を主体に進める予定です。参考書としては、
| |||||||||||||||||||||||
.jpg)
.jpg)
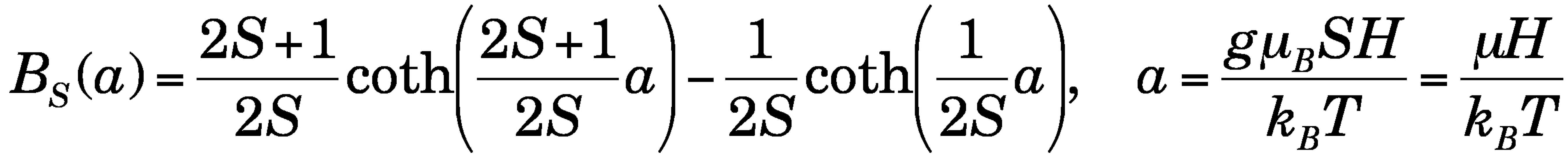
.jpg)