斜面上の質点の運動
 |
摩擦がない場合
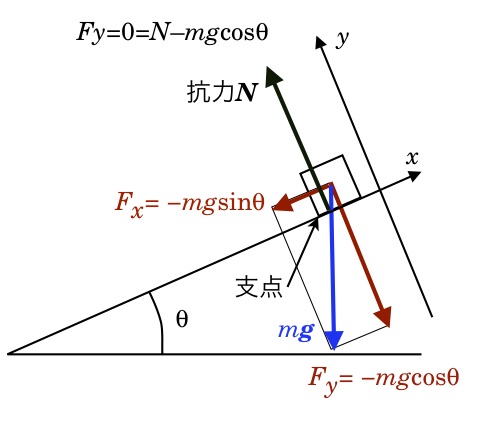
摩擦のない角度 θ の斜面を滑る質点の運動を考えよう。x–座標を斜面の上方に取り、y–座標は斜面の垂直上方に取ろう。
質点に働く力は(地球の自転などによる見かけの力を除外して考えれば)地球による重力(万有引力)mg のみである。
斜面上の大きさの無視出来る物体は、斜面に平行な方向のみに動ける自由度が与えられているため、斜面に垂直な方向の力の合力は Fy と抗力 N がつり合い、ゼロになっている(|Fy| = |N|)。
また、質点ではなく、大きさのある物体の場合には、斜面に接するその物体の支点の回りの回転が起こってはいけない。その条件から、抗力が物体に働く位置は、重心に働く重力 mg と斜面が交わる点になる注。
斜面上の質点に働く正味の力は、 x-軸の負の方向を向いた Fx = -mgsinθ のみである。その結果、自由落下と同様に、質点は斜面下方に徐々に加速される。その時の実質的な重力加速度は、自由落下の場合の mg に対して、sinθ 倍だけ小さい。
結果として、斜面上の物体の運動方程式は、因子 sinθ 以外は、自由落下する物体と全く同一になる。力 F は、座標軸の取り方が自由落下の場合とは変わったので、それに応じて変わる:F = (-mgsinθ, N-mgcosθ, 0)。斜面上の質点の運動方程式はこの力 F を代入して、
| dP/dt = F | (1) |
であり、両辺を質量 m で割って x, y 成分に分けると、
| dvx/dt = -gsinθ | |
| dvy/dt = 0 | (2) |
| dvz/dt = 0 |
となる。両辺を時間で積分して、速度の一般解は
| vx = –gsinθ ∫ dt = –gt sinθ + Cx | |
| vy = Cy | (3) |
| vz = Cz (Ci:積分定数. i = x, y, z) |
で与えられ、もう一度時間で積分すると、位置座標の一般解は
| x =–gt2sinθ/ 2 + Cxt + C'x | |
| y = Cyt + C'y | (5) |
|
z = Czt + C'z (C'i:積分定数. i = x, y, z) |
と求まる。これらの一般解は、時刻 t = 0 の初期位置や初速度の「初期条件」を未だ特定していない任意定数を含むため「あらゆる具体的な初期条件に対応した、全ての可能な」斜面上の質点の運動を表現している。
「具体的な初期条件」として任意定数が特定されると、初めてその初期条件に対応した、特解が得られることになる。
摩擦がある場合の斜面上の質点の運動
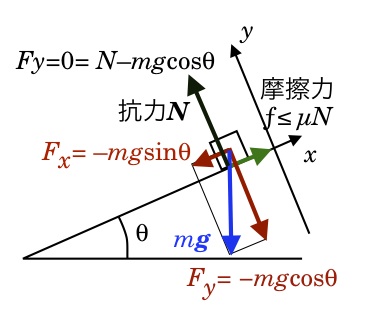 |
質点と斜面の間に摩擦力が働く場合を考えよう。摩擦力の大きさは、抗力 N の大きさに比例することが知られている。摩擦力の原因は、質点と斜面上の原子間、或いは分子間の引力または斥力である。表面が粗い場合には、凸凹同士が反撥し合うために加速が妨げられる。一方、原子の配列レベルまで滑らかである場合には、原子間の引力によって張り付いてしまい、斜面に平行な外力も完全に打消される。摩擦の物理は、現在でも、原子間力顕微鏡(AtomicForceMicroscope: AFM)のような微視的な測定手段により研究が続けられている。
摩擦力の原因から考えて、摩擦力が加速度を産み出すような事はあり得ないが、外力を打ち消したり弱める効果がある。打ち消すことが出来る最大の摩擦力を、最大 (静止) 摩擦力 fmaxと呼び、摩擦係数 µ と抗力 N を用いて ƒmax = µN (µ の定義式で、無次元量)と表される。従って、右図のような条件で、質点が斜面を滑り出すためには、Fx が最大摩擦力 µN よりも大きくなる斜面の角度が必要になる。即ち、滑り出す条件は、
| mg sinθ > µN |
で与えられる。抗力 N は常に重力の斜面に垂直な成分と等しいので、
| sinθ > µ cosθ, → tanθ > µ |
が質点が斜面上を滑り始める角度になる。斜面上の摩擦係数が場所によらず一定であれば、実質的な効果としては、斜面上の重力加速度を弱める因子 sinθ に更に摩擦の因子が加わり、(sinθ–µ' cosθ) の因子だけ重力加速度を弱める。なお、静止時に働く最大摩擦力 µcosθ と、滑り始めた後の摩擦力 µ'cosθ とは必ずしも同じ係数になるとは限らないことが知られている
注 実際には摩擦があり、滑らない条件を満たす場合のみ支点の回りの回転が生じる。回転運動の原因を与えるのは、力のモーメント N である。力のモーメントの大きさは、支点から力が働く点までの位置ベクトル r と力のベクトル F の外積で与えられる:N = r × F 。外積の定義から、その大きさは |N| = rF sinθ で与えられる。ここで、角 θ (≤ π) は、2つのベクトルが成す角度。
この例では、力のモーメントの原因になり得る力として、Fx, Fy, N の3つがある。物体の長さを b、高さを a とすると、r => F の方向が時計回りの場合を正とすると、力のモーメントの合計は、|N| = mgcosθ を使って、
N = Fyb/2 + N(b/2 - (a/2)tanθ) - Fxa/2
= (mgb/2)cosθ - mg(b/2 - (a/2)tanθ)cosθ - (mga/2)sinθ = 0
と打消す事が確認出来るので、抗力の働く点が、重心に働く重力と斜面とが交わる点である事が確認される。
07.5.21