
HOME |
導電性高分子の電子状態 − 電子スピン共鳴の視点から |
Electronic states has been studied in fully-doped conjugated polymers with electron spin resonance (ESR) technique. Integrated intensity and line width deduced from ESR spectra give us information on the electronic states of various conductive polymers. The integrated intensity provides us spin susceptibility and the ESR line width does information on dynamics of spin carriers in terms of relaxation via several interactions between the electron spins and the lattice, such as Elliott and spin diffusion mechanisms. The fully-doped conductive polymers usually show the Pauli-like, temperature-independent susceptibility with small Curie-one, called Curie-tail. Two different origins of the Curie-tail in conductive polymers are proposed to account for two kind of temperature dependences, named as categories A and B, in terms of disorder. Spin dynamics studies through the ESR line width provide us microscopic transport properties and demonstrated that the polymers in category A, covering such as polyacetylene and polypyrrole, exhibit metallic transport properties down to 2 K. However, the other polymers in category B, such as poly-p-phenylenevinylene-H2SO4 and polyaniline-camphorsulfonicacid, fall into the localized non-metallic states at low temperatures where the Pauli susceptibility disappears.
導電性高分子の電子状態の研究は、この20年にわたって多くの実験手段を用いて進められてきた [1].この報告では、高濃度にドープして金属的になっていると考えられる種々の導電性高分子について、これまでに電子スピン共鳴(ESR)法を用いて得られた結果に系統的な解釈を試みた [2].ESRスペクトルから得られるパラメーターの与える情報を表1に整理した.また、本稿で取り扱う導電性高分子の構造式と略称を図1に示す.

導電性高分子は大きく2種類に分類出来る:縮退系と非縮退系.トランス型ポリアセチレンに代表される縮退系高分子においては、その構造の対称性から、2重結合の位相を反転(1重結合と2重結合を入れ替える)をさせても構造の変化は起こらないため、その基底状態のエネルギーは縮退している.一方、図1の他の高分子は、結合交代の位相反転に対して構造が保存せず、基底状態のエネルギーも縮退していない.
|
|
|
この2種類の高分子にアルカリ金属やハロゲンなどをドープして電荷担体を導入すると、図2に示すような特徴的なスピン磁化率の濃度依存性を示す.この差異は、未ドープの縮退系に特有な、図3に示した中性ソリトンの存在にある.中性ソリトンは、ドーピングにより荷電ソリトンに変換されるため低濃度領域でスピン数が急減する.一方、非縮退系では、低濃度ではドープされた電荷がポーラロンとして蓄えられるために、濃度に比例してスピン磁化率が増加する.
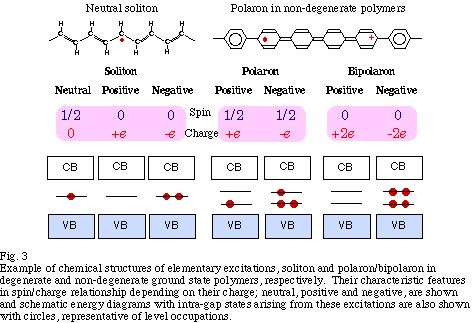
どちらの系でも、中間濃度では荷電ソリトン、或いはバイポーラロンの生成のため、スピン磁化率はほぼゼロ(縮退系)或いは急減する.しかし、高濃度にドープ(炭素原子当り数%程度以上)すると温度に依存しないパウリ的磁化率を示す.また同時に、多くの場合に低温領域でキュリー的な寄与が観測されることが知られている [1].
図1に示された種々の骨格を持つ高分子に種々のドーパントをドープすると、10桁前後の電気伝導度の上昇、パウリ磁化率の出現などが観測される.しかし、その電子状態の解明には幾つかの困難がある.その一つは単結晶が作れないために避けられない、導電性高分子の高次構造に起因している.常温における電気伝導度の値は金属と考えることが自然なほどに高いが(ヨウ素をドープしたポリアセチレンの例:〜105 S/cm)、電気伝導度は 100 K 程度までは温度降下と共に増加して、それ以下では減少するなど [3]、高次構造の影響を受けない結晶内の振舞いは十分解明されていない.
本稿では、ESRを導電性高分子に適用し、その電子状態の解析を行った.表1に示すように、ESRスペクトルの面積からはスピン磁化率が、また、線幅からは、その原因である緩和機構の解析から、スピンを持つ電荷担体の輸送特性を反映したダイナミクスを調べることが出来る.スピン磁化率の解析は、パウリ磁化率と共に低温で表われるキュリー磁化率の起源として、試料の結晶性に関連して2つ考えられることを示唆した:1.格子の強い乱れを持つ非晶質領域に孤立したポーラロンと、2.高温領域ではパウリ磁化率を示す非局在電子が、低温で弱い乱れの存在のためにアンダーソン局在を起こして出現する、キュリー磁化率とパウリ磁化率の間のクロスオーバー.線幅の解析結果は、スピン磁化率の結果と一致し、クロスオーバーを示す系では、結晶全体に分布した弱い格子の乱れのために鎖間結合が弱く、強い1次元性を示し、低温では絶縁化する様子が観測された.
スピン磁化率は、外部磁場のみを変えることにより同一周波数でESRとNMR(主に水素原子核)のスペクトルを測定し、それらの面積を比較して求めた.この方法は、シューマッハ・スリクター法と呼ばれ [4]、同一試料内のNMRを利用するため、ESR強度を校正する外部試料を要しない特徴を持つ.通常は、測定周波数は50MHz前後を用いる.
線幅は、目的により種々の周波数で測定した.表1に示すスピン拡散を調べるには、10MHz以下から20GHz以上の広い周波数に渡って測定を行う必要がある.スピンを持つ電荷担体が高分子結晶などの異方性的な結晶空間を拡散運動すると、双極子磁場などに起因する揺動磁場を感じる.ESRの緩和率は、その揺動磁場スペクトル中のラーマー周波数成分に比例する [5].測定された周波数スペクトルは拡散運動の異方性に依存した特徴を示し、そのパラメータの解析から異方的な電荷の輸送を知ることが出来る.この方法は、試料が多結晶であっても適用できる特徴を持つ [1,6,7].
高濃度にドープした導電性高分子で観測されるESRスペクトルは、良いローレンツ曲線であることが多いため、線幅の決定にはローレンツ曲線を非線形最小二乗法を用いてフィッティングし、精度を上げた.
図4にポリピロール(PPy)[8] とポリパラフェニレンビニレン(PPV)[9] のスピン磁化率の例を、温度の逆数に対して示す.特徴的な点として、PPyは有限のy切片を持つ直線で再現できるが、PPVは高温極限ではパウリ的、低温極限ではキュリー的な漸近線を持つことが上げられる.PPyでは、全測定温度量域において切片に相当するパウリ磁化率と傾斜に相当するキュリー磁化率の和で再現できることを意味している.一方、PPVは、両温度極限における振舞いがクロスオーバーしており、中間温度で電子状態が変化している(低温でχP が消滅する)ことを示唆する.
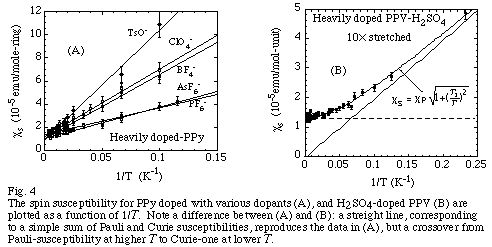
PPy以外に単純な和で再現できる系としては、種々のドーパントをドープしたポリアセチレン(PA)、ポリパラフェニレン(PPP)[10]、ポリチオフェン(PT)、そして塩酸をドープしたポリアニリン(PAni)等が上げられる.しかしながら、これらの系の中にはカリウム(K)をドープしたPAや、カンファースルホン酸(CSA)[11,12] やドデシルベンゼンスルホン酸(DBSA)をドープしたPAniのように、ドーパント種によっては硫酸をドープしたPPVと同様にクロスオーバーを示す.図4(B) に示すように、クロスオーバーは実験式
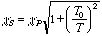 (1)
(1)
で良く再現できることが分かった [2].ここで、χP はパウリ磁化率、T0 はクロスオーバー温度である.
金属や半導体などのように、自由に動けるスピンを持つ電荷担体を持つ系では、エリオット機構と呼ばれるESRの緩和機構が知られている [13].自由な電荷担体はフォノンや格子欠陥で散乱されるが、同時に、スピン軌道相互作用の2乗に比例した確率で電子スピンが反転してスピン格子緩和を誘起し、線幅の広がり(寿命幅)として観測される:
ΔHElliott = α(λ/ΔE)2τ-1=α(Δg)2τ-1 ∝ ρ、(近似は金属の場合). (2)
ここで、α は定数係数、Δg はg−シフト、τ は電子運動量の緩和時間、ρ は電気抵抗を表す.
|
|
|
|
この機構は、半導体で観測される変化に富んだESR線幅を理解するために、Elliott によって提案された [13].(2) 式が示すように、この機構は電子運動量の緩和率に比例した線幅を与えるので、金属の場合には電気抵抗に比例する.しかし、半導体では電気抵抗はフォノン散乱のみでは決まらず、熱励起されるキャリアー数の変化などが支配するため、一般的には電気抵抗に比例するとは限らない.また、時間反転対称性のために、純粋な1次元系ではこの機構による緩和は禁止されることに注意を要する [13].図5に導電性高分子のESR線幅 ΔH の対数を、その系に含まれるスピン軌道相互作用定数 λ の対数に対して示した [2].この図の特徴は、PTやPPyのような五員環で出来た系では、五員環に窒素(PPy)を含むか或いは硫黄(PT)を含むかに大変強く依存し、ESR線幅が20倍も変わる上に、それが λ2 に比例することである.見方を変えると、ドーパントにはどんなに λ の大きな元素が含まれていても線幅には影響が表われない [14].これらの事実から、五員環高分子のESR線幅は高分子骨格内原子の λ に起因するエリオット機構が支配的であること、また、ドーパントイオンと電荷担体との相互作用が非常に弱いことが結論される [14].この結論は、PPyの結晶が五員環面同士が向き合って結合した2次元的なシート構造を持つことと良い一致を示す [15].表現を変えると、エリオット機構が観測されない系は、λ の小さな軽元素しか含まないか、1次元性がとても強いことを示唆する.(2) 式によると、線幅の温度依存性は電気抵抗に比例するはずで、金属で有れば温度上昇に伴い線幅の増大が期待できる.図6にその一例を示す.一緒にVSC抵抗の温度依存性も示すが、低温部分を除いて両者の定性的な一致は非常によい [1,14].
図5にはPAにアルカリ金属をドープした結果も示されている.興味深い点は、五員環高分子と異なり、ドーパントの l の冪上に比例する事である [16].これは、アルカリドープPAにおいては、ドーパントを介した3次元的な伝導がエリオット機構の原因になっていることを示す.五員環高分子の2次元シートと対照的に、PAではドーパントを囲むようなコラム構造を取り [17]、図5の振舞いと良く一致する.最後に、ESR線幅がエリオット機構で支配されている系のスピン磁化率が図4(A) の様なパウリ磁化とキュリー磁化の単純和で再現できることを強調しておきたい [2].
導電性高分子のように鎖内の1次元性と鎖間の相対的に弱い3次元性からなる異方的な結晶空間を電荷担体が運動する場合には、緩和時間を反映するローレンツ型のESR線幅の周波数依存性を調べることにより、電荷担体の異方的なダイナミクスを微視的に解析することが出来る [1,6,18].その特徴は、多結晶試料においても適用できる点にある.
スピンを持つ電荷担体間、或いはそれと超微細結合している核スピン間には双極子相互作用などの磁気的相互作用が働く.異方的空間内をスピンが拡散運動すると、その相互作用が時間的に変調され、異方性を反映した周波数スペクトルを与える.そのスペクトルを観測するには、スペクトルのラーマー周波数成分を与えるESR線幅(緩和率)を、広い周波数にわたって測定すればよい.例として、準一次元空間を拡散運動する場合には、ESR線幅がスペクトル密度、に比例することが示される [1,5,6].
|
|
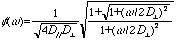 (3)
(3)
ここで、D//、D⊥ はそれぞれ鎖内、鎖間の拡散率(rad/s)で、ω はラーマー角周波数である.図7にPAniに塩酸をドープした系の例を示す.図中の曲線は (3) 式を用いて再現したもので、このフィッティングから求めた微視的な拡散率 D//、D⊥ が図8に示されている [19].直流電気伝導度も一緒にプロットしたが、その温度依存性はVariable range hopping で再現でき [20]、鎖間の拡散率の温度変化とも良く一致する事から、鎖間の拡散が伝導度の律速過程だと考えられる.一方、鎖上の拡散率は約 150 K でピークを作り、低温では半導体的で、高温になると金属的になる絶縁体・導体転移を起こす [19].
図7に示したような周波数に依存するESR線幅が観測される系としては、CSA [21](図9参照)やDBSAをドープしたPAni、硫酸をドープしたPPV [9] などがある.これらはどの系でも十分低温では絶縁体的な振舞いに変わること、スピン磁化率はクロスオーバーを示し低温では金属的なパウリ磁化が消失すること、D//とD⊥ の比が大きく1次元性が強いことなどが特徴としてあげられる.
|
|
|
|
次に、得られた実験結果の系統的な解釈を試みる.図4に示された、和:χP+χC とクロスオーバー:χP →χC はどのような物理を反映しているのだろうか.図10に解釈を試みた.図4(A) で代表される「和」を示す系、PA、PPP、PPy、PTなどでは、少なくとも部分的には、エリオット機構が有効になる高い次元(2〜3次元)の高い結晶性を持っている.また、線幅は金属的な電気抵抗に似て、温度低下と共に狭くなる温度依存性を4.2Kまで示すことが多い [1].これらの事実から、「和」で表現されるスピン磁化率は図10(a) に示したような非常に高い結晶性の領域とそれらを結ぶ非晶質部分から構成されている系だと考えられる.結晶領域にはパウリ磁化率を与える伝導電子が存在し、低温まで金属的に振舞うと同時にエリオット機構を通じて電気抵抗に比例した線幅を与える.一方、非晶質部分では曲がりくねった鎖にポーラロンが局在してキュリー磁化率を与える.孤立したポーラロンはエリオット機構のような効率的な緩和機構を持たないため、ESR線幅には大きな寄与をしない.
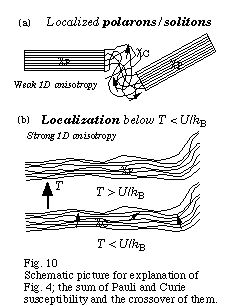 |
「クロスオーバー」を示す系では、低温領域でパウリ磁化率が消失して、キュリー磁化率に移り変わる.同時にこれらの系では、高い1次元性を反映した準1次元拡散運動に起因するスピンダイナミクスを示し、図8,9に見られるように低温領域では絶縁体的な温度依存性を示している.これらの事実から、図10(b) に示すように、弱い乱れのある系に特徴的なアンダーソン局在が「クロスオーバー」系では重要なパラメーターになっていると考えられる.試料全体にわたり弱い乱れが支配しているため、結晶性は必ずしも高くない.結果として鎖間相互作用が弱くなり高い1次元性を持つ.そのため、低温ではアンダーソン局在したポーラロンが支配的で、クーロン遮蔽も有効でなくなる.従って、有限の局在サイト内クーロン反発エネルギー U のために、パウリ原理にも係わらずフェルミ準位の状態は1つの電子によって占有され、磁化率はキュリー則に従う [22].しかし、U/k よりも温度を上げると、 U の効果は消えて磁化率の温度依存性はパウリ磁化率に変化していく [22].(1) 式のクロスオーバー温度 T0 は U/k 程度の大きさに対応していると考えられる [11].電気伝導度も、温度上昇に伴う非弾性散乱の効果によってアンダーソン局在が消失し、通常の金属的な振舞いに変わる.図9はこの様な振舞いを実験的に観測したものと理解できる.しかし、図8の塩酸をドープしたPAniのケースは鋭い転移を示していることから、アンダーソン局在とは別の機構を考える必要があるだろう.
本稿にすべての実験データを乗せることは出来ないが、表1にESRから見たときに導電性高分子の電子状態がどう見えるかを整理してみた.上の議論から結論されるように、大きく分けて2種類に分類してみることが出来る.この分類はあくまで測定した試料固有の電子状態を反映している点に注意してほしい.
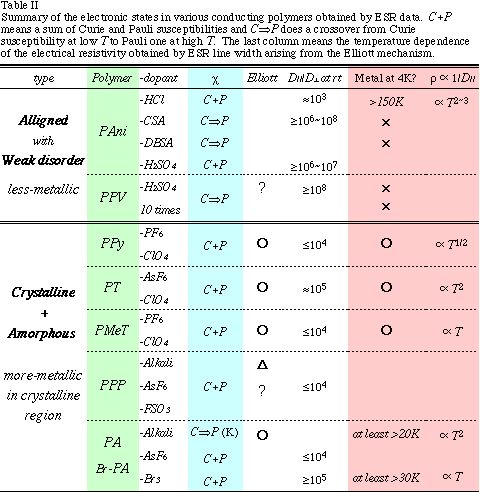
試料の合成方法や結晶化の方法論の改善に伴い、理想的には良く結晶した電子状態に収束すると期待される.部分的に高い結晶性を持つ系でエリオット機構による線幅から類推した電気抵抗の温度依存性は(右端のコラム参照)、それぞれの骨格の構造やドーパントの種類に強く影響されることが見て取れる.これらの温度依存性は、結晶内電気伝導度を観測する特殊な手法であるVSC法によっても見積もられているが、ESR線幅から得た結果ととても良い一致を示すことは解釈の妥当性を裏付けている [14].最近、Schön らによって電界効果型の素子を使って化学的なドーピングの代りに、電荷担体の電界注入を利用して絶縁体から超伝導まで電子状態を制御できるようになってきた [23]注1.また、ホールの移動度が温度の冪乗、µ ∝ T-n, n 〜1.5-2.8、に従うことも報告しており [24]、表1のデータとの類似性が今後明らかにされていくと期待されるが、電界効果素子の場合にはドーパントが結晶内には無いためドーパントポテンシャルの違いなど、興味深い点がある.一方で、本研究会で東大工学部の伊藤耕三氏が報告された有機ナノチューブ中の、ただ1本のドープしたPAniの電子状態は、ほぼ完全な1次元電子系の振舞いが観測できる可能性を提起しており、大変興味深く [25]、今後の発展が期待される.
ESR法、特に広い周波数にわたるESRを用いて導電性高分子の研究を進めてきたが、今までに得られた実験データを見直し、解析し直して全体を見渡すことを試みた.その結果、現段階で得られる導電性高分子の電子状態が大きく2つの傾向に分類できた.1つは部分的に高い結晶性を有し、必然的に異方的ではあるが高い次元性、2〜3次元、を備えている.これらは十分低温まで金属的な成分を持つことが示された.しかし、高分子骨格の違いやドーパント種の違いは、結晶構造にも反映するし、電気抵抗の温度依存性の違いともなって結果に現れてきた.また、単結晶が得られない現状では、これらの高い結晶性領域間を結ぶ非晶質部分の存在はさけられないが、その部分に局在したポーラロンの作るキュリー的な磁化として分離観測できた.しかし、通常の直流電気抵抗の温度依存性を複雑なものにするため、電子状態を研究する上では障壁となっている.一方、ESR法は結晶部分と非晶質部分の性質を分離可能にし、結晶領域の異方性まで含めた電子状態の情報が得られることを示した.
もう一つのグループは、低温でのキュリー磁化率が温度上昇と共にパウリ磁化率に連続的にクロスオーバーする特徴を持つ.この系では、鎖間の結合が十分に発達しておらず、電子状態の準1次元性が大変強く、鎖上と鎖間の拡散率の比が8桁も違うことが見出された.これらのことは、格子の乱れが電子状態に強く反映することを示唆し、磁化率のクロスオーバーも低温領域でアンダーソン局在が支配的になることで理解できた.また、高い1次元性を持つためと考えられるが、エリオット機構の寄与は見出されなかった.
得られた電気抵抗の温度依存性は、最近開発された電界効果素子の結果と比較される.ドーパントの存在が結晶構造を乱さない利点があり、将来の発展が期待される.
本稿は、多くの方々との共同研究として進めてきた研究結果を解析したものであり、この場を借りて共同研究者の方々に謝意を表明いたします.特に、中央大学の風間重雄氏、増渕伸一氏(現・東京医大)、住友化学工業の大西敏博氏、野口公信氏、CENG の Maxime Nechtschein, Jean-Pierre Travers, 防衛大の清水文比古氏、都立大の坂本浩一氏、以上の方々には試料、議論などで大変お世話になりました.
注その後、Schön らの発表論文に捏造の疑惑が起こり、現在は取り下げられている。その後の発展としては、2006年に、低温まで金属的な振る舞いをするPANiの合成に成功したという仕事が、Nature 誌に報告された。
K. Lee, S. Cho, S. H. Park, A. J. Heeger, C.-W. Lee, and S.-H. Lee, Nature 441, 65 (2006).
References
[1] K. Mizoguchi and S. Kuroda, in Handbook of Organic Conductive Molecules and Polymers, Conductive Polymers: Spectroscopy and Physical Properties, edited by H. S. Nalwa (Wiley, Sussex, 1997), Vol. 3, p. 251.
[2] K. Mizoguchi, Synth. Metals, 119, 35-38 (2001).
[3] S. Masubuchi, S. Kazama, K. Mizoguchi, F. Shimizu, K. Kume, R. Matsushita, and T. Matsuyama, Synth. Met. 57, 4866 (1993).
[4] R. T. Schumacher and C. P. Slichter, Phys. Rev. 101, 58 (1956).
[5] M. A. Butler, L. R. Walker, and Z. G. Soos, J. Chem. Phys. 64, 3592 (1976), and C. A. Sholl, J. Phys. C 14, 447 (1981) and A. Abragam, The Principles of Nuclear Magnetism (Oxford Univ. Press, Oxford, 1961).
[6] K. Mizoguchi, Jpn. J. Appl. Phys. 34, 1 (1995).
[7] K. Mizoguchi, S. Masubuchi, K. Kume, K. Akagi, and H. Shirakawa, Phys. Rev. B51, 8864 (1995).
[8] K. Mizoguchi, N. Kachi, H. Sakamoto, K. Kume, K. Yoshioka, S. Masubuchi, and S. Kazama, Synth. Met. 84, 695 (1997).
[9] H. Sakamoto, N. Kachi, F. Shimizu, K. Mizoguchi, K. Kume, T. Ohnishi, and T. Noguchi, Synth. Met. 84, 681 (1997).
[10] K. Kume, K. Mizuno, K. Mizoguchi, K. Nomura, Y. Maniwa, J. Tanaka, M. Tanaka, and A. Watanabe, Mol. Cryst. Liq. Cryst. 83, 1317 (1982).
[11] N. S. Sariciftci, A. J. Heeger, and Y. Cao, Phys. Rev. B49, 5988 (1994).
[13] R. J. Elliott, Phys. Rev. 96, 266 (1954), Y. Yafet, in Solid State Physics, edited by H. Ehrenreich, F. Seitz and D. Turnbull (Academic, N.Y., 1965), Vol. 14, p. 1.
[14] K. Mizoguchi, M. Honda, N. Kachi, F. Shimizu, H. Sakamoto, K. Kume, S. Masubuchi, and S. Kazama, Solid State Commun. 96, 333 (1995), and 増渕伸一、溝口憲治、応用物理 65, 270 (1996).
[15] Y. Nogami, J.-P. Pouget, and T. Ishiguro, Synth. Met. 62, 257 (1994).
[16] F. Rachdi and P. Bernier, Phys. Rev. B33, 7817 (1986), and Bernier, C. Fite, A. El-Khodary, F. Rachdi, K. Zniber, H. Bleier, and N. Coustel, Synth. Met. 37, 41 (1990).
[17] H. Baughman, L. W. Shacklette, N. S. Murthy, G. G. Miller, and R. L. Elsenbaumer, Mol. Cryst. Liq. Cryst. 118, 253 (1985), and Chen, M. J. Winokur, Y. Cao, A. J. Heeger, and F. E. Karasz, Phys. Rev. B45, 2035 (1992).
[18] K. Mizoguchi, M. Nechtschein, J.-P. Travers, and C. Menardo, Phys. Rev. Lett. 63, 66 (1989).
[19] K. Mizoguchi and K. Kume, Solid State Commun. 89, 971 (1994).
[20] A. J. Epstein, J. M. Ginder, F. Zuo, R. W. Bigelow, H.-S. Woo, D. B. Tanner, A. F. Richter, W.-S. Huang, and A. G. MacDiarmid, Synth. Met. 18, 303 (1987).
[21] (a): M. C. Itow, T. Kawahara, N. Kachi, H. Sakamoto, K. Mizoguchi, and K. Kume, Synth. Met. 84, 749 (1997), and (b): B. Beau, J. P. Travers, F. Genoud, and P. Rannou, Synth. Met. 101, 778 (1999).
[22] H. Kamimura, Prog. Theor. Phys. Suppl. 72, 206 (1982).
[23] J. M. Schön, A. Dodabalapur, Z. Bao, C. Kloc, O. Schenker, and B. Batlogg, Nature 410, 189 (2001).
[24] J. M. Schön, C. Kloc, and B. Batlogg, Phys. Rev. Lett. 86, 3843 (2001).
[25] E. Ikeda, Y. Okumura, T. Shimomura, K. Itho, and R. Hayakawa, J. Chem. Phys. 112, 4321 (2000).