戻る

連振り子はいくつまで動くか２？（07/3/23、19:00。）

反撥係数

　いくつまで連振り子が動くか？の問に答えるには、球同士の衝突の際に、どれだけ持っていた運動エネルギーを次の球に伝えられるか？に答えなくてはなりません。衝突の際に、音になったり、熱になったり、衝突の角度がずれて無駄な運動をしたり、と言ったことが実際には起こるため、100％の運動エネルギーは必ずしも次の球へは伝えられません。その度合いを現すのが「反撥係数、e 」になります。全ての球の質量が同じ時に、前の球の持っていた速度が、次の球にどれだけ伝わるか、という１に対する割合になります。球同士の質量のバラツキも、実際には運動量を100％伝えていく際の損失になります。

　今回、Gの嵐・驚きの実験スペシャル２で、実際に1000個の連振り子を作成し、実験が行われました。この結果から、どの様なことが分かるのか、ここで検討しましょう。

オンエアーのビデオ（抜粋:約7MB, 1.4MB）

100 個の連振子

　以前に、嵐の宿題で、嵐の大野君の工作の成果を見ました。そして、番組担当のスタッフ上野さんによりますと、念のために放映後に注意深く作って試してみた結果、100個でも、かなりの高さ（正確には伺っていないのですが9割程度）上がることを確かめられた、との伝聞を書きました。それが、以下のビデオで確認できます。8-9割方上がっているように見えます（と言うか、残念ながら、画面が切れて見えません m(_ _)m ）。 さて、仮に、反撥係数が、0.999だとすると、100個進む内に、端から順番に100回衝突します。その度に、速度が0.999倍になるので、

0.999ｘ0.999ｘ0.999ｘ・・・ｘ0.999

と、100回掛けて、

0.999の100乗=0.905

になります。エネルギーは　速度 の２乗に質量を掛けて２で割ればよいので、最初に振り子を手で持ち上げた高さに対する割合を考えるのであれば、最初の１²=１に対して、0.905を２乗した程度の高さ、即ち、

始めの高さの 0.82 倍位の高さになり、ビデオの100回の様子に近いようです。

1000 個の！特大！連振子

　この結果を1000回の場合に当てはめてみるには、0.905をさらに10回かけてやれば良さそうです。すなわち、(0.999)¹⁰⁰⁰=(0.999)¹⁰⁰¹⁰=(0.905)¹⁰=0.368 となりますので、２乗して、0.135 程度の高さまでは上がって良さそうです。 しかし、1000個のボールを並べたビデオを見ると、なんとなんと！たったの 0.5 mm 程度しか動きませんでした。これは予想外に早い減衰です。

　約150 mm の振り子が 0.5 mmしか振れないのですから、角度にしてほんの 0.2度程度になります。では、どの位の高さ上がったかというと、約 5.5 x 10^-6 mm しか上がらなかった計算になります^注１。この高さは、

100個の結果から予測した値よりも、約１万分の１も小さい

です。これは何故でしょうか？

何故、1000 連振子は 100 連振子と違うのか？

　原因はいくつか考えられます。

鋼鉄球の反撥係数が本当は小さかった。 全て同じ質量だと思った鋼鉄球は、実は質量にバラツキがあった。 それぞれの鋼鉄球の並びが不揃いで、隣り合う球の中心線が水平に並んでいなかった。

等が考えられます。順番に検証してみましょう。

1. もし、反撥係数が本当に小さいのであれば、1000個の時の高さから逆算すると、反撥係数は、0.988 程度になります。この値で100個の場合を計算すると、球の速度は最初の球と比べて、(0.988)¹⁰⁰=0.298 となり、上昇する高さは、0.09 と、10％位しか上がらないはずです。これは、ビデオの様子の10分の１位で、明らかに実験結果は

   反撥係数が 0.988 よりも、もっと大きい

   ことを示唆しています。

2. 隣接する鋼鉄球の質量が同じでないと、全ての運動量が次の鋼鉄球に伝わりません。簡単な計算から、隣接する鋼鉄球の質量の差 Δm と質量 m の比を、δ=Δm/m と書いてみます。そうすると、反撥係数が仮に１であっても、次の鋼鉄球の速度は、(1-δ/2) 倍だけ遅くなってしまいます^注２。鋼鉄球の質量のバラツキを調べてはいませんので、確定的な結論は出せませんが、金属の工作技術の一般的なレベルを考えると、約 22 mm （放送では、1000個で約 22 m と説明しているので、その1000分の一）の千分の一よりは高い精度で作られていると予想できます。そうすると、体積にして約千分の三だけばらつくので、質量のバラツキに起因する反撥係数は、約 0.997 程度以上であると予想されます。1000個では、0.0025 位或いはそれ以上は上がるはずだと分かります。これは、角度にして４度程で、距離にして10 mm 程度振れることに相当します。従って、

   質量のバラツキでは説明できない

   ことになります。しかし、逆に、工作精度が千分の四よりも低い場合には、質量のバラツキによって説明できることになりますが、１番で考えたように、100個の結果を見ると質量とは考えにくそうです。

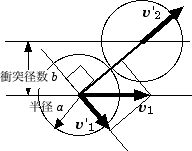3. さて、最後の衝突する２つの球の中心がずれている場合を考えてみましょう。球の半径を a、中心線のズレを b とします。そうすると、摩擦が無い場合の衝突の図１から予測できるように、球の中心の速度の方向と、２つの球の中心を結ぶ軸との成す角 θの正弦は、sinθ=b/2a で求まることが分かります。これを使うと、この場合の有効な反撥係数は、(1-(b/2a)²) で与えられることになります^注３。さて、実際にはどの程度、隣接球の中心線はズレているのでしょうか？1000個のビデオを見てみると、結構、うねって並んでいることが分かります。さすがに難しい、と言うか、1000個も並べるには根気を続けるのは大変だと思います。エーイ、もういいや、となってしまうのが人情でしょう。

   さて、中心線のズレはどの程度小さくないといけないのでしょうか？100個の場合は、有効反撥係数は、約 0.999 でした。これは、結構厳しいです。(b/2a)² が、千分の一よりも小さくないといけません。千分の一の平方根ですから、約 3% ですね。直径 2a が約 20 ｍm なので、約 0.6 mm よりも小さくなくてはいけません。しかし、1000個のデータを説明するには、全ての隣接球の中心が、さらに10倍も大きな、10％ほどズレている必要があります。それ程のズレが常にあるかどうかは？？です。従って、

   中心線のズレのみでは実験結果を説明するのは難しそう

   です。

結論

以上の考察から、これら以外にも100個から1000個に増加した時に、減衰を早める要素がありそうです。例えば、吊っている糸の固定端と鋼鉄球の中心がズレている場合などです。また、1000個を買い集めたので、

製造メーカーの異なる衝突球が含まれていたり、ロットが異なるために、球の直径が異なる部分がある

など、思いもよらぬ因子が効いているのかも知れません。何故ならば、100個と1000個の結果の違いの大きさが、なかなか

物理的なバラツキの範囲では説明が付けがたい

感があるからです。この辺りは、作った担当者に当たってみないと解決しませんが・・・

しかし、この通常では成し得ない規模の実験の成果として、

鋼鉄球の反撥係数は、0.999 よりは十分大きい

と言うことが分かった、と言えます。

^注１何故ならば、sinθ≈ 0.5/150 なので、初めの高さを１とした時の1000個目のボールが登った高さは、1-cosθ=1-(1-sin²θ)^1/2=1-(1-(0.5/150)²)^1/2=5.5x10^-6で与えられる。

^注２摩擦が無い場合の衝突の計算に於いて、どちらかの質量を m(1+δ) として解く。その際に、δ²に比例する項は、元々δが１よりもズーと小さい量なので、その２乗はもっともっと小さくなることから、ゼロと置いてしまう近似をする。

^注３２つめの球の有効な速度 v'₂は、１つめの球の運動方向成分のみであることは、摩擦が無い場合の衝突の図１から明らかでしょう。そうすると、有効な速度は cosθ が２回掛かるので、v'₂=v'₁ cos²θ = v'₁ (1-sin²θ) = v'₁ (1-(b/a)²) となることが分かります。

Index

# 07/4/1

戻る