単振動の運動方程式
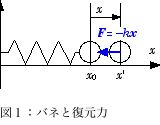 |
天井から吊した振り子やバネの先に付けた錘の運動は、単振動の運動方程式を満たす。最も単純な系は理想的なバネである。右図のように、質量の無視できるバネの先端に付けた質量 m の質点の平衡位置 x0 から x=x'-x0 だけバネが伸ばされると、それに比例した平衡位置へ戻ろうとする復元力 F= – kx が質点に働く。従って、運動方程式は、
| d2x/dt2 = F/m = – (k/m)x | (1) |
となる。
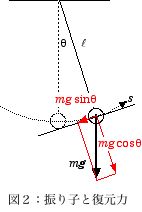 |
同様に図2の様に、天井から吊した質量の無視できる長さ l の糸の先端に質量 m の質点を付けた振子も、振動の振幅が小さい場合には、近似的に単振動と考えて解析することが出来る。質点に働く力は重力のみである。振り子の運動は、点線で表した弧上のみに限定された束縛運動になる。そこで、質点の位置の弧の接線方向と糸の方向に重力を分割して考える。糸方向成分 mg cosθ は、糸の張力と釣り合い、質点の運動には寄与しないので、接線方向成分 mg sinθ のみを接線方向の運動方程式に考慮しよう。弧上の変位 s は、振り子の平衡位置からの振れ角 θ と s = lθ の関係にあるので、運動方程式は、
| d2s/dt 2 = l d2θ/dt 2 = F/m = – g sinθ | (2) |
となる。ここで、l = const. を使った。θ << 1 (rad) の仮定の元で sinθ ≈ θ の近似を行い(注:角度は無次元量。半径 (radius)で測った弧の長さが radian (rad) )、
| d2θ/dt 2 = – (g/l) sinθ ≈ – (g/l) θ | (3) |
と整理できる。変数が x と θ の、及び、右辺の係数 (k/m) と (g/l) の2つの見かけの違いを除けば、 (1) と (2) は同一の微分方程式であることが分かる。即ち、これらの微分方程式は、
| d2x/dt 2 = – ω02x |
と書くことが出来る。ここで、ω02 は、単位変位、単位質量当たりの復元力を表し、単振動の最も大事なパラメータである。バネの場合には、ω02 = k/m で、(1) 式第2辺、第3辺から単位質量 m、単位変位 x 当たりの復元力 (= F/mx = k/m) であることは容易に分かる。単振り子の場合も、単位質量 m、単位変位 lθ 当たりの復元力 (= F/mlθ = g/l) は容易に確認できる。
これらの運動方程式を解く時に、時間について両辺を直接積分する事は出来ない。なぜならば、右辺の x は時間の関数 x(t) であり、どの様な関数であるかは、単振動の運動方程式を解かなければ決定できないからである。即ち、x(t) を求めたい時に x(t) を直接時間 t では積分出来ない事は自明である。そこで、2つの解法を見ていこう。一つは、発見的方法で、もう一つはエネルギー積分の方法である。
1)発見的方法
運動方程式 (1) を見ると、求めたい関数 x(t) を時間で2回微分すると、負号を付けた元の関数 x(t) に比例している。この様な関数は、三角関数か指数関数以外には無いことに注目して、
| x(t) = A sin ωt + B cos ωt | (4) |
と置いてみる。運動方程式 (1) を満たすA, B, ω の条件を求める事が出来れば、それが運動方程式の解であることは明らかであろう。ここで、A, B は積分変数であり、運動方程式が時間の2回微分方程式である事から、2つの積分変数が必要になる。
次に、(4) 式が運動方程式を満たすべき条件を探すために、 (1) 式に代入する。すると、左辺は
| d2x/dt 2 = –ω2(A sin ωt + B cos ωt) = –ω2x |
と求まる。右辺と等しいので、
| ω2 = k/m = ω02 |
が、(4) 式が運動方程式を満たすための条件になる。即ち、
| x(t) = A sin ω0t + B cos ω0t |
が運動方程式 (1) の一般解を与える。一般解とは、2回積分した分の積分定数を含む解であり、任意の初期条件の元で、バネや振り子の運動を表現できる。
一般解に初期条件を代入すると、その初期条件の特(別)解が得られる。例えば、変位 x0 で固定した状態から、時刻 t=0 に初速 v=0 で運動を開始する場合は、
| x(0) = B = x0 | |
| v(0) = dx/dt |t=0= ω0 (A cos ω0t – B sin ω0t) |t=0 = ω0A = 0 |
から、
| x(t) = x0 cos ω0t | |
| v(t) = –ω0x0 sin ω0t |
が求まる。一方、時刻 t = 0 で x = x0、v = v0 の場合には、
| x(0) = B = x0 | |
| v(0) = dx/dt |t=0= ω0 (A cos ω0t – B sin ω0t) |t=0 = ω0A = v0 |
より、この場合の特解は、
| x(t) = (v0/ω0) sin ω0t + x0 cos ω0t | |
| v(t) = v0 cos ω0t – ω0x0 sin ω0t |
と得られる。また、時刻 t=0 で x=0、v=v0 の場合には、
| x(t) = (v0/ω0) sin ω0t | |
| v(t) = v0 cos ω0t |
2)エネルギー積分を使う方法
エネルギー積分とは、運動方程式
| m d2x/dt 2 = – kx |
を積分する際に、両辺に速度 v = dx/dt を掛けて積分する方法を指す。その結果がエネルギーの次元を持つ事から、エネルギー積分と呼ばれる。
| mv (d2x/dt 2) = – kxv = – kx (dx/dt) | |
| mv (dv/dt) = – kx (dx/dt) | (5) |
両辺に dt を掛けて積分すると、
| mv2/2 = m ∫ v dv = – k∫ x dx = – kx2/2 + const. | (6) |
が得られる。左辺は錘の運動エネルギーを、右辺の第1項はバネの位置エネルギーを表し、左辺に移項すると、全運動エネルギーが時間によらず一定、というエネルギー保存則になっている事が分かる。積分定数を const. = kC2/2 と書き換えると、
| (dx/dt)2 = (k/m)(C2 – x2) | |
| dx/dt = (k/m)½(C2 – x2)½ | (7) |
と変形できる。最後の式を見ると、右辺は x のみの関数なので、両辺を (C2 – x2)½ で割って dt を掛けると変数が両辺に分離され、両辺を積分することが出来る(変数分離法)。
| ∫ (C2 – x2)-½ dx = ±(k/m)½ ∫ dt | (8) |
この積分を更に進めるために左辺の変数変換を行う。
| x = Csinθ |
と置くと、dx = Ccosθ dθ 、また、(C2–x2)½ = Ccosθ となり dx と打ち消し合い dθ だけ残る。結局、(8) の左辺は、
| ∫ (C2–x2)-½ dx = ∫ dθ = θ (= sin-1(x/C)) (逆三角関数) |
と積分でき、位相角 θ に等しいことが分かる。t ≥ 0 に対応して θ ≥ 0 の領域を選べば (8) は
| θ = ω0 ∫ dt = ω0 t + φ (ω0 = (k/m)½) |
となり、単振動の一般解として
| x = Csin(ω0t + φ) |
が得られる。
|
Csin(ω0t + φ) = C (cosφ sinω0t + sinφ cosω0t) = A sinω0t + B cosω0t、 (A = C cosφ、B = C sinφ) |
から、「1)発見的方法」で求めた一般解に等しい解が求まる。
# 07.8.24