
HOME |
ジャンボジェット機の揚力の運動量保存則による考察 |
○飛行機の翼の役目は、運動量保存則から考えると、空気に下方への運動量を持たせ、逆に翼が上向きの運動量を得ることにある.
○翼は、空気に対して進行方向にはその運動量を変化させないと仮定する.すなわち、上下方向のみの運動量を与えると考える.翼は後縁に向かって下がっており、空気がなめらかに翼に沿って流れれば、自然と下方向きの運動量を得ることになる.簡単のために、翼を通過した後、空気が下方45度の運動量を持つとしよう.ジャンボジェット機が離陸をするためには、速度v が
 |
 |
v = 300 km/h 〜 83 m/s
になる必要がある.その時、空気の下方への速度成分は、
vd = v•sin(π/4) 〜 0.7v となる.
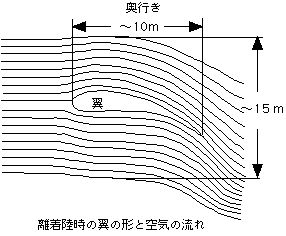
○さて、毎秒あたり、どれだけの質量 M の空気が下方への運動量を持つか見積もる必要がある.翼の全幅 w は約 50 m ある.また、翼の平均の奥行き D は 10 m 程度だと考え、翼の上下に奥行きと同程度、すなわち、厚さ t が 15 m 程度の空気層がその運動量を斜め下方に変えると仮定する.そうすると、密度 ρ = 1.3 kg/m3 、速度 v = 83 m/s を用いて、単位時間にその層を通過する空気の質量は、
M/Δt = ρ•v•w•t = 1.3•83•50•15 = 8.1•104 kg/s (1)
となる.そうすると、空気の得る下方への単位時間あたりの運動量(=力)は、重力加速度を g = 10 [m/s2] として、
F = ΔP/Δt = M•vd/Δt = 8.1•104 •83•0.7 = 4.7•106 [kg•m/s2 = N] = 470 [ton]•g [m/s2] = MF•g (2)
で与えられ、揚力荷重 MF は 470 トンと得られる.これは、ジャンボジェット機の最大荷重約 400 トンに匹敵しており、これらの考察が合理的な見積を与えていると考えられる.
○推力荷重の見積でも同様であるが、運動量を下方に変える空気層の厚さ、空気層の下方への速度成分の大きさ等の見積には数十から100%程度の曖昧さがあり、厳密には運動方程式を用いて数値計算により見積もる必要がある.
○以上の考察は、流体力学的な考察と比較される.翼の形状から上側の空気流が早くなり、エネルギー保存則からその分だけ圧力が下がる(運動エネルギー、圧力による仕事、位置エネルギーの合計が一定:ベルヌーイの定理.非圧縮性流体に適用できる理論だが、非常に早い流れでは定性的な傾向は正しいと期待される.).翼面積は 400 m2 以上あることを考えると、1気圧の圧力差により 4,000 トンの揚力になるので、離陸時には 0.1 気圧程度の翼上下面における圧力差が生じていると期待される.
○揚力を生み出すために生ずる、翼の部分の空気の下方流は、翼端の部分に渦巻きを生じさせることが知られている.翼の直後の部分の空気の下方流の上側では圧力が下がり、翼の外側から空気を引き込み、その下側では加圧された空気が外側に押し出されるためである.