HOME |
親子ボール |
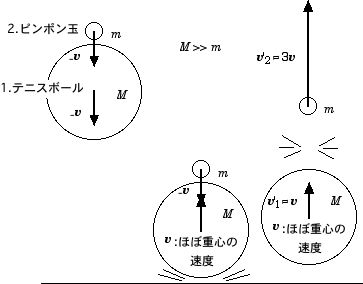
下図のように、大きくて重い硬式テニスボールの上に軽くて小さいピンポン玉を載せたまま自由落下させ（下図左）、床に衝突した後の振舞いを観察しよう．上手くピンポン玉がテニスボールの中心に保てれば、ピンポン玉だけを床で弾ませた場合に較べると遥かに高く、最大で９倍くらい高くまで弾むのを観察できる．
その理由を考えてみよう．議論を簡単にするために、床との反発係数 e は１（弾性衝突）としよう．概念的には次のように説明できる．テニスボールの質量 M はピンポン玉の質量 m よりも十分に重いので、親子ボールの重心の位置は、ほぼテニスボールの重心（中心）にある．さて、テニスボールが床で反射された直後を考えよう（下図中央）。まず最初に、テニスボールが直前に持っていた速度 -v （鉛直上方を正に取っている）は v に変化する．即ち、床との衝突後の重心の速度は上方に v だと考えて良い．ここで考えているのは、テニスボールは床に衝突したが、ピンポン玉はまだテニスボールに衝突する直前の瞬間である。テニスボールは上向きに速度 v でピンポン玉は下向きに -v であるため、両者は相対速度 2v の正面衝突をすることになる．親子ボールの重心がほぼテニスボールの中心にあるため、重心に対する相対速度 -2v を持つピンポン玉の衝突は、静止した壁に弾性衝突するのと同じ振舞い、速度 -2v から 2v への変化，をする．即ち、ピンポン球は親子ボールの重心から速度 2v で離れていく．重心自身は速度 v で運動しているので、結局、ピンポン玉は 2v+v=3v で床から離れていく．
ピンポン球が弾む高さは、テニスボールと衝突した直後に持っていた運動エネルギー
|
次に、力学的エネルギー保存則と運動量保存則を使って式で予測しよう．
保存力場（ここでは重力場）内で運動する限り、位置の変化に伴う重力ポテンシャルの変化分は運動エネルギーの変化分とちょうど打消すので、運動エネルギーと位置エネルギーの和は親子ボールの衝突前後で変化しない．又、衝突直前と直後を較べると、位置エネルギーは変化しないので、前後の運動エネルギーの和が保存する：
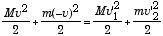 . | (1) |
左辺は図の中央の絵に相当し、右辺は右の絵の状態を表す．この２つの絵の間には、親子ボール間の衝突以外には外からは力が働くことはない．この時には運動量も保存する：
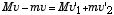. (2)
(2) 式を
Mv'1 = -mv'2 - mv + Mv (3)
と変形して(1) 式に代入すると、
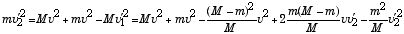
となり、両辺を整理すると、
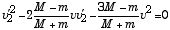
が得られる．これを解いて
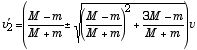
となる．M >> m の条件下では、
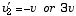が解になる。しかし、-v は衝突せずに通過する場合なので物理的に除外され、3v が求めるピンポン玉の速度になる。確認のために M=m の場合を考えてみると、
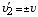（「トンネルしない」条件から、v のみが物理的に合理的な解）
と予想される解を与えることが確認できる。