戻る
このページは"Mathjax"を使って数式を表示しています。不都合がある場合にはこちらをどうぞ。
地上で観測される色々な現象,例えば降雨やパラシュートによる安全な降下などを半定量的に理解するために、空気,即ち流体の抵抗を考える必要がある。そこで,ここでは空気抵抗の2つの原因を考察して、ニュートン力学が現実の世界を説明出来ている事を確認しよう。
粘性抵抗
摩擦のない完全流体を除くと、流速の分布に伴う粘性抵抗が働き、粘性力は速さ $v$ の勾配に比例する。
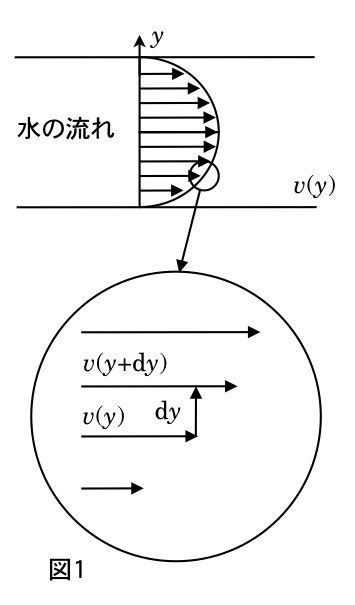
図1のように、粘性を持つ川の水の流れを考えよう.経験的に、流体と固体(川岸)の接する面では流速が0となり、川の中央ほど速くなることが知られている.そのため、$dy$ だけ離れた流線間の速さに $dv=v(y+dy)-v(y)$ の差が生ずる。$dy$ に対する流線間の速度差 $dv$ の比(速度勾配)
$$\large{
\frac{dv}{dy}=\lim_{dy\to 0}\frac{v(y+dy)-v(y)}{dy},
}$$
に比例して水分子間の衝突による粘性(摩擦)が大きくなると考えられる。川岸では常に速度が0なので、速度勾配も中央の速度 $v$ に比例する。粘性抵抗 $F$ と速度勾配の比例係数を粘性係数 $\eta$ と定義すると、流線間の単位接触面積あたりの粘性力 $\tau$ は
|
$$\large{
\tau=\frac{F}{S}=\eta\frac{dv}{dy}, \qquad (1)
}$$
|
と書き表せる.粘性係数の単位は、(1) 式から、
$${\large
\left[\eta\right]=\left[\frac{\frac{F}{S}}{\frac{dv}{dy}}\right]}=\left[\frac{{\rm N/m^2}}{{\rm s}^{-1}}\right]=\left[\rm{Pa\cdot s}\right],
$$
で与えられる.ここで、$\large{\rm{Pa = \frac{N}{m^2}}}$ は圧力の単位で、$10^3$ hPa $=10^5$ Pa が約1気圧に相当する.
一様な流速 $v$ 中に置かれた半径 $a$ の球の受ける粘性抵抗 $F$ は、近似的に、粘性応力 $\large{\tau=\eta\frac{dv}{dy}}$ に球と流体が接する表面積 $S=4\pi a^2$ を掛けて得られる:
|
$$\large{
F=S\eta\frac{dv}{dy}=4\pi a^2\eta\frac{v}{a}=4\pi a\eta v=cv, \quad (c=4\pi a\eta, \text{正確な計算によると}6\pi a\eta v) \qquad (2)
}$$
|
ここで、球の表面に接する流体の流速 ($v=0$) が、球からその半径 $a$ 程度離れれば一様な流れの速度 $v$ になると仮定し、球の表面の速度勾配を $\large{\frac{v-0}{a}}$ で近似した。この場合、粘性抵抗は速さ $v$ に比例し、20度C、1気圧の空気の粘性係数は約 $\large{1.8\times 10^{-5}}$ [Pa・s]で、水の粘性係数は、それより2桁近く大きく $\large{0.80\times 10^{-3}}$ [Pa・s]である。
 |
慣性抵抗
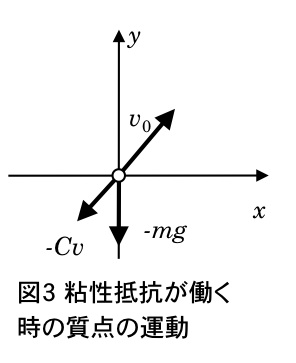
速度が遅い場合には、速度に比例する粘性抵抗が効果的であるが、ある程度速くなると(形状に依存)速度の2乗に比例する慣性抵抗が主になる.図2に示す速度 $v$ で落下する半径 $l$ のパラシュートを考えよう.このパラシュートが落下するにつれて、その下方の断面積 $S$ ($=\pi l^2$) の空気が排除される.この効果を、断面積 $S$ の空気を下方に速度 $v$ に加速すると理解出来る.即ち、単位時間の間に加速する空気の体積 $\large{\frac{\Delta V}{dt}}$ は $Sv$、その質量 $\Delta M$ は空気の密度を $\rho$として $\large{\frac{\Delta M}{\Delta t}=\rho Sv}$ となる.結果として、空気は $dt$ 時間当り $\Delta M=\rho Sv\Delta t$ と $v$ を掛けた運動量 $\large{\frac{dP}{dt}}$ を得る。結局、運動方程式 $\large{\frac{dP}{dt}=F}$ より、パラシュートの受ける慣性抵抗の大きさは $\large{F=\frac{dP}{dt}=\rho Sv^2=Dv^2}$ ($D=\rho S$) になる。方向は「摩擦」なので、常に $-v$ の方向。 この表式は近似式なので、正確にはこれに形状に依存した1程度の大きさの係数がかかる:$D=k\rho S$.
粘性抵抗がある場合の運動
速度に比例する粘性抵抗があるときには、運動方程式は速度に比例する減衰項を含み
|
$$\large{
m\frac{dv_x}{dt}=-cv_x,\quad \frac{dv_x}{dt}=-\frac{c}{m}v_x, \qquad (3a)
}$$
$$\large{
m\frac{dv_y}{dt}=-mg-cv_y,\quad \frac{dv_y}{dt}=-\frac{c}{m}\left(v_y+\frac{mg}{c}\right), \qquad (3b)
}$$
|
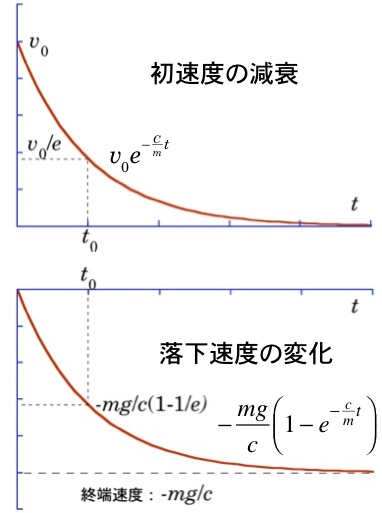
と書ける.$\large{t_0=\frac{m}{c}}$ $\left[\large{\rm{\frac{Kg}{N/\frac{m}{s}}}}\right]$=[s] は、慣性の大きさと摩擦による減速の比率で決まる時定数(速度が $\large{\frac{1}{e}}$ に減速されるに要する特性時間)である.慣性質量が大きければ摩擦に負けないため、減速までの時間が長くなる事に対応する。(3a) 式の両辺を $v_x$ で割り $dt$ を掛け、変数を左辺は $v_x$、右辺は $t$ に変数分離する。同様に (3b) 式を $v_y+\frac{mg}{c}$ で割り $dt$ を掛け、変数を左辺は $v_y$、右辺は $t$ に変数分離する。両式をそれぞれの変数で積分して、
$$\large{
\int \frac{dv_x}{v_x}=-\frac{c}{m}\int dt, \quad \ln{|v_x|}=-\frac{c}{m}t+C_x, \quad v_x=Ae^{-\frac{c}{m}t}=Ae^{-\frac{t}{t_0}}, \quad (A=e^{C_x})
}$$
$$\large{
\int \frac{dv_y}{v_y+\frac{mg}{c}}=-\frac{c}{m}\int dt, \quad \ln{|v_y+\frac{mg}{c}|}=-\frac{c}{m}t+C_y, \quad v_y=Be^{-\frac{c}{m}t}-\frac{mg}{c}=Be^{-\frac{t}{t_0}}-\frac{mg}{c}, \quad (B=e^{C_y})
}$$
が得られる.ここで、初期条件、$t=0$ で $v=v_0$ を代入すると積分定数が $\large{A=v_{0x}, \quad B=v_{0y}+\frac{mg}{c}}$ と決まり、
$$\large{
v_x=v_{0x} e^{-\frac{c}{m}t}=v_{0x}e^{-\frac{t}{t_0}},
}$$
$$\large{
v_y=\left(v_{0y}+\frac{mg}{c}\right) e^{-\frac{c}{m}t}-\frac{mg}{c}=v_{0y}e^{-\frac{t}{t_0}}-\frac{mg}{c}\left(1-e^{-\frac{t}{t_0}}\right),
}$$
となる.これらの結果から、初速度は時定数 $t_0$ で減衰し、落下速度は同じ時定数で終端速度に漸近する。
時刻 $t$ における質点の位置は、速度をもう一度時間で積分して、
$$\large{
x=\int dx=v_{0x}\int e^{-\frac{c}{m}t}\,dt=-\frac{mv_{0x}}{c}e^{-\frac{c}{m}t}+C_{x1},
}$$
$$\large{
y=\int dy=v_{0y}\int e^{-\frac{c}{m}t}\,dt-\frac{mg}{c}\int (1-e^{-\frac{c}{m}t})\,dt, \qquad (5)
}$$
$$\large{
\quad=-\frac{mv_{0y}}{c}e^{-\frac{c}{m}t}-\frac{mg}{c}\left(t+\frac{m}{c}e^{-\frac{c}{m}t}\right)+C_{y1},
}$$
が得られる.初期条件、$t=0$ で $x=y=0$ を代入し、 $\large{C_{x1}=\frac{mv_{0x}}{c}}$, $\large{C_{y1}=\frac{mv_{0y}}{c}+\frac{m^2g}{c^2}}$ から、
$$\large{
x=\frac{mv_{0x}}{c}\left(1-e^{-\frac{c}{m}t}\right),
}$$
$$\large{
y=\frac{mv_{0y}}{c}\left(1-e^{-\frac{c}{m}t}\right)-\frac{mg}{c}\left(t-\frac{m}{c}\left(1-e^{-\frac{c}{m}t}\right)\right), \qquad (6)
}$$
となる.$y$ の第1項は、初速度による到達距離、第2項は、摩擦のある場合の自由落下距離。
慣性抵抗がある場合の運動
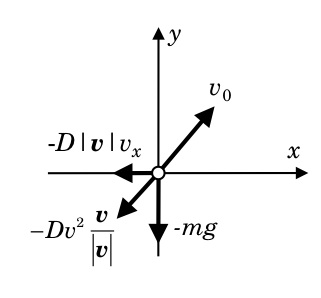 |
速度の2乗に比例する慣性抵抗がある場合の質点の運動方程式は、
$$\large{
m\frac{dv_x}{dt}=-\left(Dv^2\frac{\boldsymbol v}{|\boldsymbol v|}\right)_x=-D|\boldsymbol v|v_x,\quad \frac{dv_x}{dt}=-\frac{D}{m}|\boldsymbol v|v_x=-\frac{D}{m}v_x\sqrt{v_x^2+v_y^2},
}$$
$$\large{
m\frac{dv_y}{dt}=-mg-\left(Dv^2\frac{\boldsymbol v}{|\boldsymbol v|}\right)_y=-mg-D|\boldsymbol v|v_y,\quad \frac{dv_y}{dt}=-\frac{D}{m}\left(|\boldsymbol v|v_y+\frac{mg}{D}\right), \qquad (7)
}$$
と書ける.(7) の両式は、$v_x,\ v_y$ の両成分を含む連立微分方程式になる.ここでは、簡単のために (1) $\large{v=v_x}$(重力は働かず、摩擦のみがある慣性運動、常に $\large{v>0}$)或いは (2) $\large{v=v_y}$(摩擦のある自由落下、常に $\large{v<0}$)の場合の2通りを考えよう.
$$\large{
(1) \quad m\frac{dv}{dt}=-Dv^2, \quad \frac{dv}{dt}=-\frac{D}{m}v^2,
}$$
$$\large{
(2) \quad m\frac{dv}{dt}=-mg-Dv^2, \quad \frac{dv}{dt}=-\frac{D}{m}\left(\frac{mg}{D}-v^2\right), \qquad (8)
}$$
を変数を分離してから時間で積分して、
$$\large{
(1) \quad \int \frac{dv}{v^2}=-\frac{D}{m}\int dt, \quad \frac{1}{v}=\frac{D}{m}t+C_1, \quad v=\frac{m}{D}\frac{1}{t+\frac{mC_1}{D}},
}$$
$$\large{
(2) \quad \int \frac{dv}{\frac{mg}{D}-v^2}=-\frac{D}{m}\int dt, \quad \frac{1}{2}\sqrt{\frac{D}{mg}}\int\left(\frac{1}{\sqrt{\frac{mg}{D}}-v}+\frac{1}{\sqrt{\frac{mg}{D}}+v}\right)dv
}$$
$$\large{
=\frac{1}{2}\sqrt{\frac{D}{mg}}\left(-\ln{\left|\sqrt{\frac{mg}{D}}-v\right|}+\ln{\left|\sqrt{\frac{mg}{D}}+v\right|}\right)=\frac{1}{2}\sqrt{\frac{D}{mg}}\ln{\left|\frac{\sqrt{\frac{mg}{D}}+v}{\sqrt{\frac{mg}{D}}-v}\right|}=-\frac{D}{m}t+C_2, \qquad (9a)
}$$
が得られる.(2) の場合は常に $\large{v<0}$ で、$\large{v^2\le\frac{mg}{D}}$(終端速度の2乗)が成立ち、
$$\large{
(2) \quad \frac{\sqrt{\frac{mg}{D}}+v}{\sqrt{\frac{mg}{D}}-v}=A\exp\left(-2\sqrt{\frac{Dg}{m}}t\right), \quad \sqrt{\frac{mg}{D}}+v=\left(\sqrt{\frac{mg}{D}}-v\right)A\exp\left(-2\sqrt{\frac{Dg}{m}t}\right),
}$$
$$\large{
\qquad v=-\sqrt{\frac{mg}{D}}\ \frac{1-A\exp\left(-2\sqrt{\frac{Dg}{m}}t\right)}{1+A\exp\left(-2\sqrt{\frac{Dg}{m}}t\right)}, \quad \left(A=\exp\left(2\sqrt{\frac{mg}{D}}C_2\right)\right) \qquad (9b)
}$$
となる.初期条件、$t=0$ で (1) の場合は、$v=v_0$、(2) の場合は、$v=0$ を、それぞれに代入して得た $C_1=\large{\frac{1}{v_0}}$ と $A=1$ を代入し、
$$\large{
(1) \quad v=\frac{m}{D}\frac{1}{t+\frac{m}{Dv_0}},
}$$
$$\large{
(2) \quad v=-\sqrt{\frac{mg}{D}}\ \frac{1-\exp\left(-2\sqrt{\frac{Dg}{m}}t\right)}{1+\exp\left(-2\sqrt{\frac{Dg}{m}}t\right)}=-\sqrt{\frac{mg}{D}}\tanh\left(\sqrt{\frac{Dg}{m}}t\right), \qquad (10)
}$$
を得る.また、(2) の場合の $v$ の終端速度は $\large{-\sqrt{\frac{mg}{D}}}$ で与えられ、(8) 式の(2) で $\large{\frac{dv}{dt}}=0$ と置いて得られる結果と等しいことが確認できる.この場合の特性時間は $\large{t_0=\sqrt{\frac{m}{Dg}}}$ である.この時間の数倍でほぼ終端速度になると考えて良い.
さて、到達距離 $y$ は、(10) 式を更に時間で積分して、
$$\large{
(1) \quad y=\int dy=\frac{m}{D}\int\frac{dt}{t+\frac{m}{Dv_0}}=\frac{m}{D}\ln\left|A\left(t+\frac{m}{Dv_0}\right)\right|
}$$
$$\large{
(2) \quad y=\int dy=-\sqrt{\frac{mg}{D}}\int\tanh\left(\sqrt{\frac{Dg}{m}}t\right)\,dt=-\frac{m}{D}\ln\left|B\cosh\sqrt{\frac{Dg}{m}}t\right|, \qquad (11)
}$$
が得られる.ここで、$\ln{A},\ \ln{B}$ は積分定数.また、初期条件、$t=0$ で (1) $y=0$, (2) $y=h_0$ を代入して得た $A={\large\frac{Dv_0}{m}},\ B=\exp\left(\large{-\frac{Dh_0}{m}}\right)$ を代入し、
$$\large
(1) \quad y=\frac{m}{D}\,\ln\left|\frac{Dv_0}{m}t+1\right|, \qquad (12)
$$
$$\large
(2) \quad y=h_0-\frac{m}{D}\,\ln\left|\cosh\sqrt{\frac{Dg}{m}}t\right|=h_0-v_ft-\frac{v_f^2}{g}\,\ln\frac{1+\exp\left(-\frac{2gt}{v_f}\right)}{2}, \qquad \left(v_f=\sqrt{\frac{mg}{D}}\right) \quad (a)
$$
を得る.面白いことに、速度に比例する粘性抵抗の場合には、 $x$ 成分は有限の距離までしか飛ばないが、速度の2乗に比例する慣性抵抗の (1) 場合には、速度が小さいところで限りなくゆっくり減衰するため極限値がないが、実際には粘性抵抗の寄与が効いてくる.また、(2) の場合には、($a$) から分かるように、$t\to\infty$ の極限では $y=h_0-v_ft+{\large\frac{v_f^2}{g}}\ln{2}$ となるので、$-v_ft$ に比例して降下する.