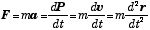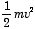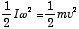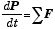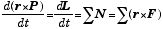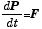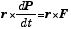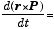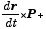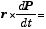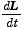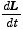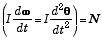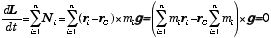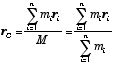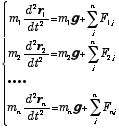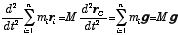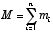回転運動を考える上で
実験的に確かめられていること:ニュートンの運動方程式
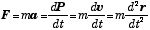
回転運動もこの運動方程式に従うはず.
回転運動の運動方程式は何故必要か?
並進運動との対比
並進運動 回転運動
| 運動の速さ | 速度 v | 角速度 ω = v/r | |
| 運動エネルギー | 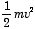 | 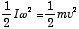 | (I = mr2) |
| 運動の激しさ | 運動量 P = mv | 角運動量 L = r×mv = Iω | |
| 運動の変化率 | 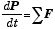 | 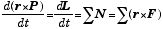 | |
並進運動でも、回転運動でも、速度 v [m/s] で運動する質点のエネルギーには変りはない.違う点は、並進運動では運動の速さを表現する指標が v であるのに対して、回転運動の場合には、角速度 ω [rad/s] である点にある.即ち、「角速度が ω 」と言ったときには、速度は ω×r [m/s] から回転半径 r に比例する.このために、回転運動を表現する物理量は、並進運動の場合と比較すると、「回転半径 r 」が入った形になる.
慣性モーメント
最初の例として、慣性質量 m [kg] と慣性モーメント I [kg • m2] を見てみよう.外力 F [N=kg • m/s2] を加えて速度 v に加速するのに要するエネルギーは、慣性質量 m に比例する.同様に、回転半径が r で質量 m の回転体に力を加えて加速し、角速度 ω = v/r にするのに要するエネルギーは、慣性質量 m に比例するだけでなく、回転半径 r の2乗にも比例する.なぜならば、その時に
| 回転体が得るエネルギーは mv2/2 だから、回転運動の保存量である ω で表現してやれば mr2ω2/2 |
(= Iω2/2(I = mr2 [kg • m2]))となるからである.この時、並進運動の慣性の大きさの「慣性質量」 m に対して、 I を回転運動の慣性の大きさ、「慣性モーメント」と呼ぶ.
角運動量
次に、並進運動の運動量 P = mv と角運動量 L = Iω の対応を見てみる.運動量 P = mv は保存量(外力が働かない限り変化しない量)であるが、常に向心力が働いている円運動では保存しない.即ち、時間と共に方向が変化する r ベクトルを含む運動量、 P = mv = mω×r 、は円運動の保存量ではあり得ない.向心力以外の外力が働いていないときに、
| 円運動で保存する量は角速度ベクトル ω と回転半径 r = |r| |
なので、運動量 P に半径ベクトル r を掛けて回転半径の2乗 r2 倍にした、角運動量ベクトル
|
L = r ×P = r ×mv = mr×(ω×r) = Iω、 (= mω(r • r) - mr(ω • r) = mr2ω = Iω, (∴ ω•r = 0))
|
が、外力が働いていない円運動の保存量になり得る.運動量 = 速度 × 慣性質量に対応して、角運動量は回転の速さ ω と回転のし難さである慣性モーメント I の積になっている.
回転の運動方程式
さて、それでは回転の運動方程式はニュートンの運動方程式とどんな関係になっているのだろうか.ニュートンの運動方程式は
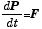 | (1) |
であったが、回転運動では運動量 P=mv の代りに角運動量 L = r×mv = Iω が向心力以外の外力が無いときに変化しない保存量なので、(1) 式を角運動量の式に変えればよい.そのために、(1) 式の両辺左側から半径ベクトル r の外積を掛けてみよう:
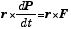 | = N |
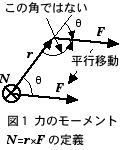
ここで、N = r×F [N • m = kg • m2/s2] は「力のモーメント」と呼ばれる.一方、左辺が
に等しいことは、この第1項の外積が、dr/dt = v と P=mv が平行(θ=0)なので、ゼロになることから分る.結局、回転の運動方程式は
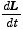 | = | 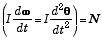 | (= rFsinθ) | (2)
|
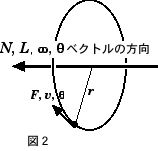
と求まる.なお、この回転の運動方程式が、テコの原理や重心の定義も与えている.ここで、ベクトル N, L, q, w の方向は、
| 回転方向が時計回りに見える位置から向う側に伸びる方向 |
で定義される.また、(2) 式は円運動だけでなく、太陽系のような中心力場における回転運動等で一般的に成立ち、向心力以外の外
力が無ければ L=const. も成立っている.(理由を考えよ)
重心
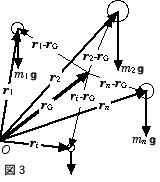
互いに内力を及ぼし合う質点の集まりが静止している.重力場中で、これらの質点の重心を支えると、重心の周りで回転運動をすることなく静止を続ける.そのような重心は (1), (2) 式によって導かれる.即ち、静止を続けるので力のモーメントのベクトル和はゼロでなければならない.図3のように、剛体(変形しない質点の集まり)中の位置ベクトル ri の質点 i に重力 mig(g は重力加速度ベクトル)が働いている場合を考えよう.回転の運動方程式 (2) 式を重力場中で考えてみると、
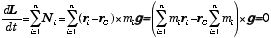
となるので、括弧内をゼロと置くことにより、重心を、
として
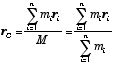 | (3) |
と定義出来る.一方、それぞれの質点の並進運動の方程式は次式で与えられる.
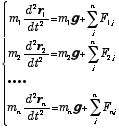 | (4) |
ここで、Fij は質点間の内力を示すので、これらを加え合わせると内力は消え、
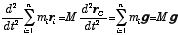 | (5) |
が得られる.ここで、M は
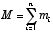
を、rG は重心の位置ベクトルを表す.即ち、剛体(変形しない質点の集まり)の運動方程式 (5) は、
| 全ての質点が重心 rGに集まっていて、そこに全重力が働いている |
場合と同じ並進運動をすることを示している.従って、重心を支えると、全重力と抗力が釣り合うので重心は静止する.
重力に加えて、激力が加わる場合の運動はもっと複雑になる.剛体の回転運動は、激力が回転中心(重心、質量中心)に対して与えた力のモーメントが決めるので、 (2) 式を用いて調べることが出来る.それから得られる回転の運動エネルギーと激力によって質点系になされた仕事の差の分が、重心の並進運動のエネルギーに変わることを利用すると、比較的容易に激力による運動を予測できる.
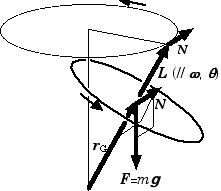
コマの歳差運動
回転の運動方程式が予測する角運動量ベクトル(回転軸の方向と平行)の時間変化は、とても奇妙な振舞いをする.すなわち、N(= rG×F) ベクトルの向きに角運動量ベクトルの方向が動いて行くが、実際に加えた力 F の方向とは垂直であるため、回転していない物体に力を加えた場合に予想される結果とは違っており、意外な感じを受ける.
コマもこの回転運動方程式に従う.コマの回転軸が傾いている場合には、良く知られているように、首振り運動(歳差運動)をする.その理由は、重心に働く重力が外力 F に相当するので、接地点から重心に向う回転半径ベクトル rG と重力 mg の外積の「力のモーメント N 」が地面と平行になるためである.それがコマの回転軸と平行な角運動量の向きを変えるので、
ことになる.
# 07.4.1