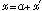 とおいて得られる ƒ(a+x') = b0 + b1x'+ b2x'2 +··· を n 回微分して、x'=0 と置くと
とおいて得られる ƒ(a+x') = b0 + b1x'+ b2x'2 +··· を n 回微分して、x'=0 と置くと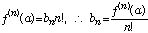 (4)
(4)となる.従って、(3)式は
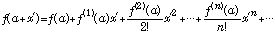 (5)
(5)となる.ここで、
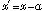 で変数を戻すと、
で変数を戻すと、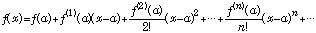 (6)
(6)が得られる.これら(5), (6)式を、
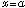 の周りのテーラー展開と呼ぶ.
の周りのテーラー展開と呼ぶ.HOME |
マクローリン展開と近似式 |
変数 x に関して何度でも微分可能な関数(無限回微分可能関数と呼ぶ) ƒ(x) が、以下のような級数
ƒ(x) = a0 + a1x + a2x2 +··· (1)
で表されるとする.ただし、a0、a1、··· は定数である.この級数を n 回微分すると、
ƒ(n)(x) = ann! +Σ∞k=1 an+1 [(n+k)!/k!] xk 、
ここで x = 0 と置くと
ƒ(n)(0) = ann!,
従って、
an = ƒ(n)(0)/n! (2)
となる.ここで、ƒ(n)(0) は、ƒ(x) を x で n 回微分し、x = 0 と置くことを意味する.(2) 式を(1) 式に代入すると、関数 ƒ(x) は
ƒ(x) = ƒ(0) + ƒ(1)(0) x + (ƒ(2)(0)/2!) x2 + ··· + (ƒ(n)(0)/n!) xn + ··· (3)
という無限級数で表すことが出来る.これを、関数 ƒ(x) のマクローリン展開と言う.
(1)式に於いて、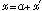 とおいて得られる ƒ(a+x') = b0 + b1x'+ b2x'2 +··· を n 回微分して、x'=0 と置くと
とおいて得られる ƒ(a+x') = b0 + b1x'+ b2x'2 +··· を n 回微分して、x'=0 と置くと
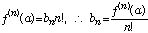 (4)
(4)
となる.従って、(3)式は
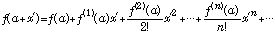 (5)
(5)
となる.ここで、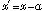 で変数を戻すと、
で変数を戻すと、
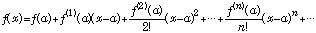 (6)
(6)
が得られる.これら(5), (6)式を、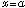 の周りのテーラー展開と呼ぶ.
の周りのテーラー展開と呼ぶ.
 が小さいときには
が小さいときには の高次項が無視できるので、(3)、(6)式を利用してƒ(x) の近似式を得ることが出来る.
の高次項が無視できるので、(3)、(6)式を利用してƒ(x) の近似式を得ることが出来る.
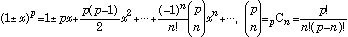 (二項係数) (7)
(二項係数) (7)
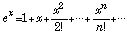 (8)
(8)
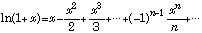 (9)
(9)
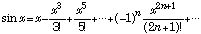 (10)
(10)
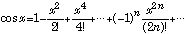 (11)
(11)
問 各自これらの展開を確認せよ.
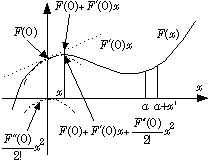
任意の何回でも微分可能な関数、即ち、何回微分しても滑らかな関数であれば、冪上の無限級数で表現可能である.0の周りの展開では、x が小さければF(x)はF(0)で良く近似される.更に、x の接線F'(0)を使いF'(0)•x を加えると更に近似が高くなる.次にx=0でF(x)に接するF(0)+ F'(0)x +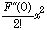 とすれば更に良くF(x)を再現できる.マクローリン展開が成立つことは、次数を上げていくと幾らでも正確にF(x)を再現できる事を示す.テーラー展開は、同じ事をx=aで考えればよい.
とすれば更に良くF(x)を再現できる.マクローリン展開が成立つことは、次数を上げていくと幾らでも正確にF(x)を再現できる事を示す.テーラー展開は、同じ事をx=aで考えればよい.
 |
この性質を利用したのが近似式である.なにか比較する量と較べて(比較対象が存在することが大切)x が十分に小さければ、最初の補正項はマクローリン展開の第一項、F'(0)xまで残せば十分である事が多い.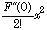 の項はx が1よりも小さければ小さいほどx に対して無視できるようになる.もちろん、x が偶然に消えてしまって残らないときには次の項
の項はx が1よりも小さければ小さいほどx に対して無視できるようになる.もちろん、x が偶然に消えてしまって残らないときには次の項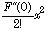 を残す必要がある.そうしないと何も残らないから...
を残す必要がある.そうしないと何も残らないから...
よく使う近似式は、式(8)〜(11) のx の1次まで残した、
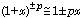 ,
, 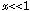
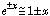 ,
, 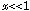
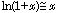 ,
, 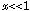
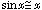 ,
, 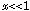
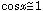 ,
, 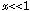
などである.