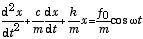
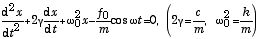(1)

で与えられる非同次微分方程式になる（右辺が０の時に同次（斉次）微分方程式と呼ぶ）．一般的に強制振動の場合は、単振子の固有振動数 ω₀ ではなく ω で振動する。また、摩擦は揺れを遅らせるため、外力の振動（ω）より位相が遅れる． 単振動を表現する方法として、実軸上の位相差を用いた三角関数による方法（図１）の代りに、演算が取り扱いやすい複素平面内の回転（e^iωt）により表現する方法（図２、実際の振動は実軸への射影）が便利である．ここで、微分の効果を考えてみると、三角関数では、cosωt を微分すると –ω sinωt に変わり、位相が π/2 だけ進むが、複素平面では、e^iωt が微分で iω e^iωt に変わり、i = e^iπ/2 なので π/2 だけ回転することになる（他の例は：1 = eⁱ⁰、–1 = e^iπ、–i = e^i3π/2）．

複素ベクトル表示

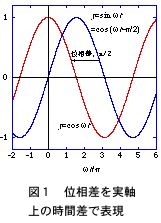
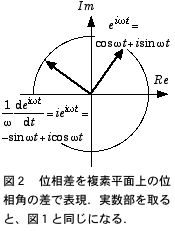
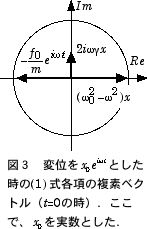
　そこで x = x₀ e^iωt と置くと、(1) 式の微分方程式の時間に依存しない定常解は複素平面内のベクトル和で理解出来る．t = 0 の時には、図３の様に外力を ƒ₀ cosωt = ƒ₀ Re{e^iωt} と複素ベクトルの実数部分に対応させる前提で ƒ₀e^iωt とし、t = 0 の瞬間の図を書くと、
（１）バネの復元力の項、ω₀² x と、２回微分で位相が π だけ回転する加速度の項は、外力と同様に実軸上のベクトル、
（２）一方、時間の一回微分の速度に比例する摩擦項は iωe^iωt となり、複素平面上で位相が π/2 だけ回転した虚軸上のベクトル、
になる．変位の振幅 x₀ を実数とすると、摩擦がない時は（γ = 0）(1) 式の全ての項は実軸上のベクトル（図３）なので、 x = x₀ e^iωt の振幅 x₀ を調整すれば (1) 式が０になる解を見つけられる．ところが、摩擦項が加わると、図３に示すように各項の長さをどのように調節しても x₀ が実数である限り、３つの複素ベクトル（加速度+摩擦+復元力）と外力ベクトルとをつり合わせることは出来ない． しかし、 x₀ も複素数にして位相シフトを考えれば、図４の例のように、(1) 式の（加速度+摩擦+復元力）を外力ベクトルとつり合わせることが可能になる．

強制振動の特別解

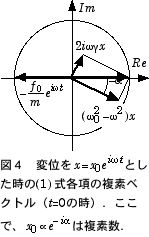
　摩擦項がない時、t = 0 で全てのベクトルが実軸上に（任意の時間では一直線上に）来るため、定常状態の特別解は x = x₀ e^iωt を(1) 式に代入して x(t) = ƒ₀e^iωt/m(ω₀²–ω²) となる．一方、速度に比例する摩擦項が有限になると 2iωγx 項が虚軸に現れ、その増加につれて x の位相の遅れ –α が増加する．即ち、速度に比例する摩擦項の効果により振動の位相に外力からの遅れが生じてくる．考えている系に損失がある場合には、一般的に応答が遅れ、外力の振動数が系の共振周波数 ω₀、或はそれ以上になると顕著になる．
　(1) 式に定常解として予想される関数系 x = x₀ e^i(ωt–α)（複素数部分は振動の位相として e^–iα に出したので、 x₀ は実数に取って良い）を代入すると、

–ω²x + 2iγωx + ω₀²x – (ƒ₀e^iα/m)(x/x₀) = [ω₀²–ω² + 2iγω – (ƒ₀/mx₀)(cosα + isinα)]x

= {[ω₀²–ω²–(ƒ₀/mx₀) cosα] + i[2γω–(ƒ₀/mx₀) sinα]}x = 0

と整理できる．x としてゼロでない解が存在するためには、実部、虚部それぞれがゼロになる必要があるので、連立方程式

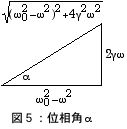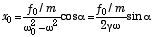、　 を解くことにより、x₀ と α が決定でき、定常状態の特別解は、
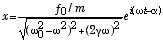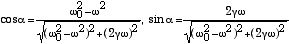、 (2)

で与えられる．

強制振動の一般解

　さて、非同次微分方程式、(1) 式の一般解は、(2) 式の特解に、外力を０として得られる同次微分方程式：

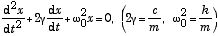　　　(3)

の一般解を加えて得ることが出来る．この式の解は、外力がなく、摩擦がある時の振動なので、初期条件で与えられた振動の振幅が時間と共に減衰をする「過渡現象」を表す。その過渡現象が納まった後に、外力による「定常的な振動」が残ることになる。

　(3) 式を複素ベクトルで考えてみると、外力がないので x = x₀ e^i(ω₀t-α) の様な単振動解を仮定しても、図３から想像できるように α と x₀ をどの様に調整しても摩擦に起因する虚部を打ち消すことは出来ない．そのため、解の形として x = x₀ e^{(–γ±iω)t} を考える必要がある．ここで、e^–γt の項は、振動解を時間と共に減衰させる重みを与える（「減衰振動」）．微分してみると分かるように、e^(–γ+iω)t は摩擦の第２項から –2γ²x + 2i γωx と位相が π/2 進んだ（時間軸で見ると、時間的に遅れた）虚数ベクトル成分を出すが、２回微分する第１項の加速度は (–γ + iω)²x = (γ²–ω²)x–2i γωx と、丁度虚数部を打ち消す特徴を持つために実数部だけでなく、虚数部もゼロにする事が可能になる．これは、振動振幅を徐々に減らす事によって、摩擦による時間の遅れを挽回していると言えよう。

　さて具体的には、x = e^λt と置いて求めた (3) 式の特性方程式 (λ²+2γλ+ω₀²)x = 0 を解いて得た

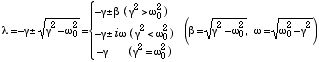
を用いて、最初の２つの場合は、２つの任意定数を含む一般解（「過減衰解」と「減衰振動解」、共に実数解）

x_β(t) = e^–γt (x₁e^βt + x₂e^–βt) = x₀ e^–γt cosh(βt + α), (γ² > ω₀²), tanhα = (x₁–x₂)/(x₁+x₂)

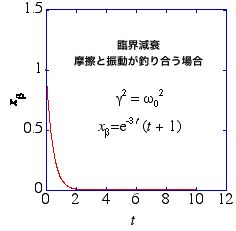
x_ω(t) = e^–γt (x₁e^iωt + x₂e^–iωt) = x₀ e^–γt cos(ωt + α), (γ² < ω₀²), tanα = –i(x₁–x₂)/(x₁+x₂) 　　　　　(4)

を得ることが出来る。

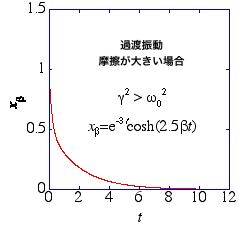
　しかし、３番目の重根解、γ = ω₀ の場合は２階微分方程式に対して一つの独立な関数 e^–iγt しか得られないため、２つの積分定数を持つ一般解が作れない。そこで、e^–iγt の係数が時間で変化すると考える「定数変化法」を用いる。即ち、x = y(t) e^–iγt, γ = ω₀ と置いて (3) に代入すると、γ², γ の項は互いに打ち消し合うので、

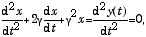
と y(t) の２階微分の項のみが残り、２回積分して y(t)= at+b を得る。結局、(4a) と共に

x = (at + b) e^–γt

が２つの任意定数を持つ一般解として得られる。(4b) の解は「臨界減衰解 (critical damping)」と呼ばれる。

　x_β(t) は摩擦項が単振動項よりも強く、１回振動しない内に振幅が減衰してしまう場合で「過減衰解 (overdamping)」を、x_ω(t) は摩擦が弱く、何回か振動している内にだんだん減衰して消えていく「減衰振動解 (damping oscillation)」を与える．なお、x_ω(t) が実数である条件は、x₁ = x₂^* (複素共役）で、また、x₀ = {2(x₁²+x₂²)}^½ である．e^–γt の因子は、速度に比例する摩擦によって生ずる、「振幅の減衰」を表し cosh(βt+α) 及び cos(ωt+α) は初期条件で決まる振動の因子になる．(2) 式と(4) 式を加えたものが(1) 式の強制振動の一般解を与える．

戻る

# 07/5/24